Chứng minh rằng : \(\left(2005+2005^2+2005^3+...+2005^{10}\right)\) chia hết cho 2006

Những câu hỏi liên quan
chứng mimh : M= ( 2005 + 2005^2 + 2005^3 +....+ 2005^10) chia hết cho 2006
2005 (1+2005)+20053 (1+2005)+..+20059 .(1+2005)
=2005.2006+ 20053.2006+...+20059 .2006
=2006 (2005+20053+...+20059) chia het cho 2006
Đúng 1
Bình luận (0)
Cho A = 2005 + 20052 + 20053 + 20054 + 20055 + 20056 +......................... 20059 + 210 . Chứng minh rằng: A chia hết cho 2006
Chứng minh rằng:
a) C = 2 + 22 + 2 + 3 +...+ 299 + 2100 chia hết cho 31
b) M = (2005 + 20052 + 20053 +...+ 200510) chia hết cho 2006
c) 2x + 3y chia hết cho 17 <=> 9x + 5y chia hết cho 17
Chứng minh
a, M=2005+20052+......+200510chia hết cho 2006
b,A=3+32+......+3100chia hết cho 40
a)M=2005+20052 +.....+200510
=>M=(2005+20052 )+.....+(20059 +200510 )
=>M=2005(1+2005)+.....+20059 (1+2005)
=>M=2005*2006+.....+20059 *2006
=>M=2006(2005+...+20059 ) chia hết cho 2006(đpcm)
b)A=3+32 +....+3100
=>A=(3+32 +33 +34)+....+(397 +398 +399 +3100 )
=>A=3(1+3+32 +33 )+....+397 (1+3+32 +33 )
=>A=3*40+...+397 *40
=>A=40(3+...+397 ) chia hết cho 40(đpcm)
Đúng 0
Bình luận (0)
Cho frac{a}{b}frac{c}{d}. Chứng minh:a) frac{left(a-bright)^3}{left(c-dright)^3}frac{3a^2+2b^2}{3c^2+2d^2}b)frac{4a^4+5b^4}{4c^4+5d^4}frac{a^2b^2}{c^2d^2}c)left(frac{a-b}{c-d}right)^{2005}frac{2a^{2005}-b^{2005}}{2c^{2005}-d^{2005}}d)frac{2a^{2005}+5b^{2005}}{2c^{2005}+5d^{2005}}frac{left(a+bright)^{2005}}{left(c+dright)^{2005}}e)frac{left(20a^{2006}+11b^{2006}right)^{2007}}{left(20a^{2007}-11b^{2007}right)^{2006}}frac{left(20c^{2006}+11d^{2006}right)^{2007}}{left(20c^{2007}-11d^{2007}right)^{20...
Đọc tiếp
Cho \(\frac{a}{b}=\frac{c}{d}\). Chứng minh:
a) \(\frac{\left(a-b\right)^3}{\left(c-d\right)^3}=\frac{3a^2+2b^2}{3c^2+2d^2}\)
b)\(\frac{4a^4+5b^4}{4c^4+5d^4}=\frac{a^2b^2}{c^2d^2}\)
c)\(\left(\frac{a-b}{c-d}\right)^{2005}=\frac{2a^{2005}-b^{2005}}{2c^{2005}-d^{2005}}\)
d)\(\frac{2a^{2005}+5b^{2005}}{2c^{2005}+5d^{2005}}=\frac{\left(a+b\right)^{2005}}{\left(c+d\right)^{2005}}\)
e)\(\frac{\left(20a^{2006}+11b^{2006}\right)^{2007}}{\left(20a^{2007}-11b^{2007}\right)^{2006}}=\frac{\left(20c^{2006}+11d^{2006}\right)^{2007}}{\left(20c^{2007}-11d^{2007}\right)^{2006}}\)
f)\(\frac{\left(20a^{2007}-11c^{2007}\right)^{2006}}{\left(20a^{2006}+11c^{2006}\right)^{2007}}=\frac{\left(20b^{2007}-11d^{2007}\right)^{2006}}{\left(20b^{2006}+11d^{2006}\right)^{2007}}\)
ừ, bạn bik làm thì giúp mình nha ^^
Đúng 0
Bình luận (0)
Cho S= 2005 + 2005 ^2 + 2005^3 +......+ 2005^2006
chứng minh rằng s chia hết cho 4022030
câu này 4 ai trả lời sớm đúng mình xin kết bạn nha { mà dấu ^ là mũ đó nha}
\(A=2005^{2007^{2006}}+2006^{2005^{2007}}+2007^{2006^{2005}}\)
Chứng minh rằng A chia hết cho 102( lưu ý không sử dụng đồng dư thức để chứng minh)
Chứng minh: (n+20052006) (n+20062005) chia hết cho 2
Chứng minh:
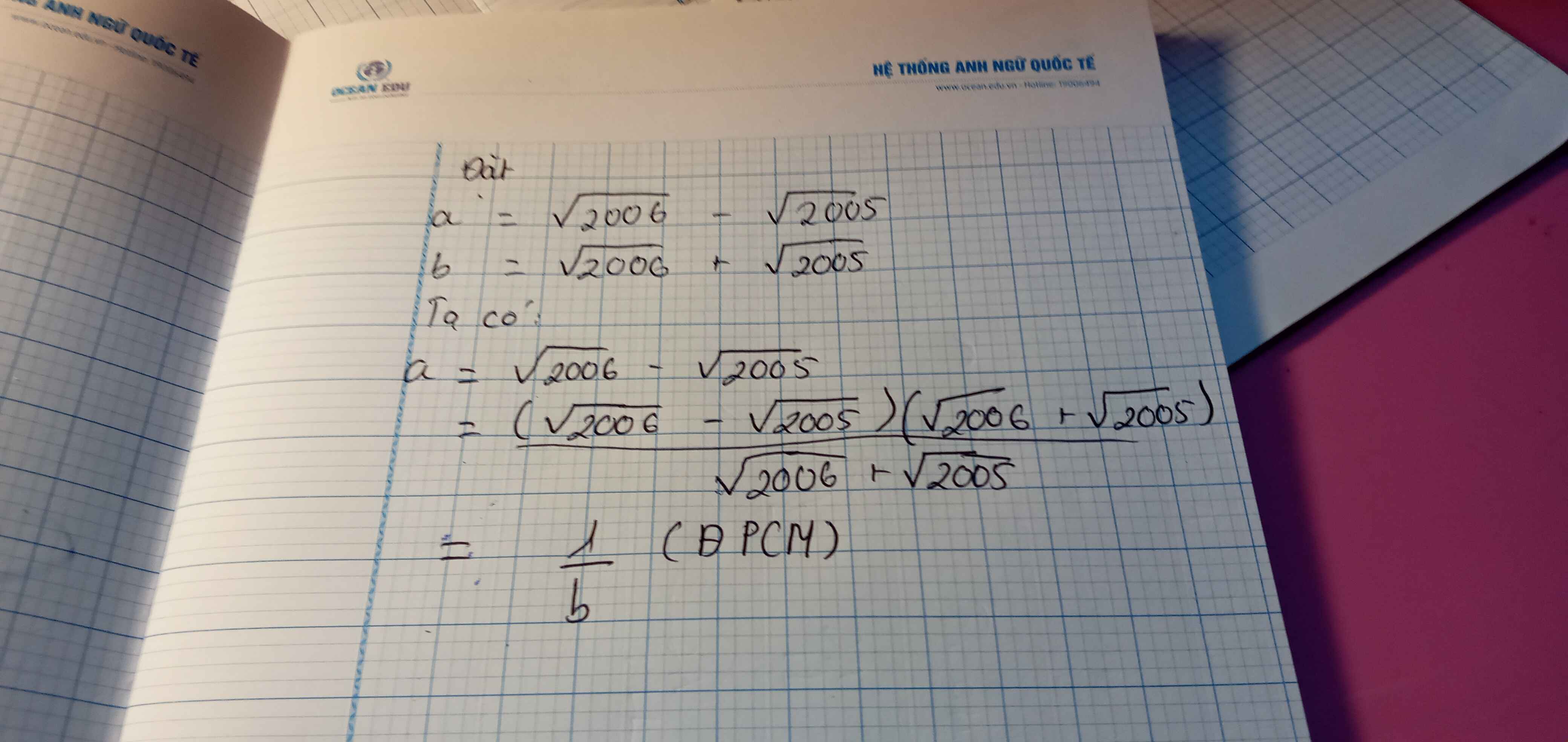
\(\left(\sqrt{2006}-\sqrt{2005}\right)\)và \(\left(\sqrt{2006}+\sqrt{2005}\right)\)là 2 số nghịch đảo của nhau.
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)
Ta có
\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)
\(\RightarrowĐfcm\)
Đúng 6
Bình luận (1)
\(\sqrt{2006}-\sqrt{2005}=\dfrac{1}{\sqrt{2006}+\sqrt{2005}}\)
Do đó: \(\sqrt{2006}-\sqrt{2005};\sqrt{2006}+\sqrt{2005}\) là hai số nghịch đảo
Đúng 2
Bình luận (0)