ai giup minh voi mai phai nop roi

câu 1 

xét tích 3 số

=(3a^2.b.c^3).(-2a^3b^5c).(-3a^5.b^2.c^2)

=[3.(-2).(-3)].(a^2.a^3.a^5).(b.b^5.b^2).(c.c^3.c^2)

=18.a^10.b^8.c^5 bé hơn hoặc bằng 0

=>tích 3 số đó không thể cùng âm=>3 số đó ko cùng âm dc

bây giờ mk đi học rùi tí về mk làm típ nhá

a) Khi $a=3$, ta có phương trình:
$$x-3x+3-x+3x-3+3^2+3^3-3^2=0$$
$$\Leftrightarrow 6x=51 \Leftrightarrow x=\frac{17}{2}$$
Vậy nghiệm của phương trình là $x=\frac{17}{2}$.

b) Khi $a=1$, ta có phương trình:
$$x-x+1-x+1x-1+3+1-1=0$$
$$\Leftrightarrow x=0$$
Vậy nghiệm của phương trình là $x=0$.

c) Để phương trình có nghiệm $x=0,5$, ta cần giải phương trình:
$$0,5-a(0,5)+a-0,5+a(0,5)-a+3a^2+a^3-a^2=0$$
$$\Leftrightarrow a^3+3a^2-2a=0$$
$$\Leftrightarrow a(a-1)(a+2)=0$$
Vậy các giá trị của $a$ để phương trình có nghiệm $x=0,5$ là $a=0,1$ hoặc $a=-2$.

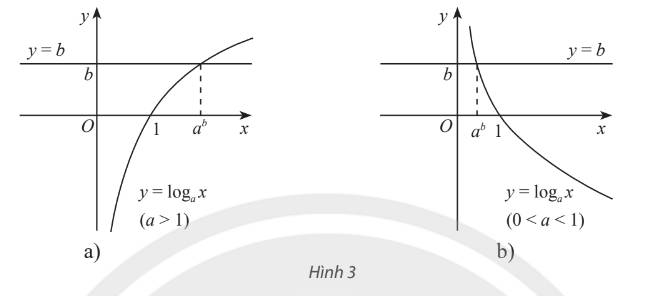
tham khảo.

Đồ thị của hai hàm số \(y=\log_ax\) và \(y=b\) luôn cắt nhau tại một điểm duy nhất. Khi đó phương trình \(\log_ax=b\)  có nghiệm duy nhất \(x=a^b\).

https://hoc24.vn/hoi-dap/question/177629.html (câu 2)

\(Sửa đề a=1/(căn 3 của 3) -1 \)

Bài 1 : 

\(N=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)

Ta có : \(x+y+z=0\Rightarrow x+y=-z;y+z=-x;x+z=-y\)

hay \(-z.\left(-x\right)\left(-y\right)=-zxy\)

mà \(xyz=2\Rightarrow-xyz=-2\)

hay N nhận giá trị -2 

Bài 2 : 

\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)Đặt \(a=10k;b=3k\)

hay \(\frac{30k-6k}{10k-9k}=\frac{24k}{k}=24\)

hay biểu thức trên nhận giá trị là 24 

c, Ta có : \(a-b=3\Rightarrow a=3+b\)

hay \(\frac{3+b-8}{b-5}-\frac{4\left(3+b\right)-b}{3\left(3+b\right)+3}=\frac{-5+b}{b-5}-\frac{12+4b-b}{9+3b+3}\)

\(=\frac{-5+b}{b-5}-\frac{12+3b}{6+3b}\)quy đồng lên rút gọn, đơn giản rồi 

1.Ta có:\(x+y+z=0\)

\(\Rightarrow\hept{\begin{cases}x+y=-z\\y+z=-x\\x+z=-y\end{cases}}\)

\(\Rightarrow N=\left(x+y\right)\left(y+z\right)\left(x+z\right)=\left(-z\right)\left(-x\right)\left(-y\right)=-2\)

2.Ta có:\(\frac{a}{b}=\frac{10}{3}\Rightarrow\frac{a}{10}=\frac{b}{3}\)

Đặt \(\frac{a}{10}=\frac{b}{3}=k\Rightarrow a=10k;b=3k\)

Ta có:\(A=\frac{3a-2b}{a-3b}=\frac{3.10k-2.3k}{10k-3.3k}=\frac{30k-6k}{10k-9k}=\frac{k\left(30-6\right)}{k\left(10-9\right)}=24\)

Vậy....

1. a = 3 thì phương trình trở thành:

\(\frac{x+3}{3-x}-\frac{x-3}{3+x}=\frac{-3\left[3.\left(-3\right)+1\right]}{\left(-3\right)^2}-x^2\)

\(\Leftrightarrow\frac{\left(x+3\right)^2+\left(3-x\right)^2}{\left(3-x\right)\left(3+x\right)}=\frac{-3\left[-9+1\right]}{9}-x^2\)

\(\Leftrightarrow\frac{x^2+6x+9+x^2-6x+9}{\left(3-x\right)\left(3+x\right)}=\frac{-3.\left(-8\right)}{9}-x^2\)

\(\Leftrightarrow\frac{2x^2+18}{9-x^2}=\frac{24}{9}-x^2\)

\(\Leftrightarrow\frac{2x^2+18}{9-x^2}+x^2=\frac{24}{9}\)

\(\Leftrightarrow\frac{2x^2+18+9x^2-x^4}{9-x^2}=\frac{24}{9}\)

\(\Leftrightarrow\frac{11x^2+18-x^4}{9-x^2}=\frac{24}{9}\)

\(\Leftrightarrow99x^2+18-9x^4=216-24x^2\)

\(\Leftrightarrow9x^4-123x^2+198=0\)

Đặt \(x^2=t\left(t\ge0\right)\)

Phương trình trở thành \(9t^2-123t+198=0\)

Ta có \(\Delta=123^2-4.9.198=8001,\sqrt{\Delta}=3\sqrt{889}\)

\(\Rightarrow\orbr{\begin{cases}t=\frac{123+3\sqrt{889}}{18}=\frac{41+\sqrt{889}}{6}\\t=\frac{123-3\sqrt{889}}{18}=\frac{41-\sqrt{889}}{6}\end{cases}}\)

Lúc đó \(\orbr{\begin{cases}x^2=\frac{41+\sqrt{889}}{6}\\x^2=\frac{41-\sqrt{889}}{6}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\pm\sqrt{\frac{41+\sqrt{889}}{6}}\\x=\pm\sqrt{\frac{41-\sqrt{889}}{6}}\end{cases}}\)

Vậy pt có 4 nghiệm \(S=\left\{\pm\sqrt{\frac{41+\sqrt{889}}{6}};\pm\sqrt{\frac{41-\sqrt{889}}{6}}\right\}\)

Sửa)):

a = -3 mà ghi lôn a = 3.giải tương tự như 3

b)

Đề: Cho a, b, c > 0 và abc = ab + bc + ca. Chứng minh rằng: \(\frac{1}{a+2b+3c}+\frac{1}{2a+3b+c}+\frac{1}{3a+b+2c}\le\frac{3}{16}\)

~ ~ ~ ~ ~

\(abc=ab+bc+ca\)

\(\Leftrightarrow1=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)

Áp dụng BĐT \(\frac{1}{x+y}\le\frac{1}{4}\left(\frac{1}{x}+\frac{1}{y}\right)\), ta có:

\(\frac{1}{a+2b+3c}+\frac{1}{2a+3b+c}+\frac{1}{3a+b+2c}\)

\(\le\frac{1}{4}\left(\frac{1}{a+c}+\frac{1}{2\left(b+c\right)}+\frac{1}{2\left(a+b\right)}+\frac{1}{b+c}+\frac{1}{2\left(a+c\right)}+\frac{1}{a+b}\right)\)

\(=\frac{1}{4}\left[\frac{3}{2\left(a+c\right)}+\frac{3}{2\left(b+c\right)}+\frac{3}{2\left(a+b\right)}\right]\)

\(=\frac{3}{8}\left(\frac{1}{a+c}+\frac{1}{b+c}+\frac{1}{a+b}\right)\)

\(\le\frac{3}{32}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)

\(=\frac{3}{16}\) (đpcm)

Dấu "=" xảy ra khi a = b = c