Xét ΔABC có 

M là trung điểm của AB

N là trung điểm của AC

Do đó: MN là đường trung bình của ΔBAC

Suy ra: MN//BC

Xét tứ giác BMNC có MN//BC

nên BMNC là hình thang

Giải

Ta thấy đường trung bình tam giác ABC nên BEDC là hình thang, lại có\(BM=MC\cdot DN=NC\Rightarrow MN\)   là đường trung bình hình thang BEDC hay MN ong song DE và BC. Lại dùng đường trung bình thì 

\(MI=KN=\frac{DE}{2}\left(1\right)\)

\(MN=\frac{DE^2+BC}{2}\Rightarrow IK=MN-2MI=\frac{DE+BC}{2}-DE\)

\(=\frac{BC-DE}{2}=\frac{DE^2}{2}\left(BC=2DE\right)\left(2\right)\)

\(\Leftrightarrow Q\cdot E\cdot D\Rightarrowđcpm\)

Mình sẽ làm câu b trước rồi từ đó suy ra a
b)Giả sử MP=PQ=QN đã có từ trước
Xét △△ ABC có E là trung điểm AB,D là trung điểm AC \Rightarrow ED là đường trung bình của △△ ABC\Rightarrow ED//BC và ED=BC/2(*)
Xét hình thang EDBC có M là trung điểm BE,N là trung điểm CE \Rightarrow MN//BC( (*) (*) )
Từ (*)( (*) (*) ) \Rightarrow ED//MN
Xét △△ BED có M là trung điểm BE,MP//ED \Rightarrow MP là đường trung bình của △△ BED \Rightarrow MP=ED/2
Tương tự cũng có NQ=ED/2
Ta có :MP=PQ
\Leftrightarrow ED2=BC−ED2ED2=BC−ED2
\Leftrightarrow ED=BC-ED
\Leftrightarrow 2ED=BC
Tương tự với NQ và PQ cũng rứa
Vậy muốn NQ=PQ=MP thì 2ED=BC Điều này là hiển nhiên ở (*)
từ đó phát triển lên câu a)NQ=PQ=MP=1/2ED
\Rightarrow MN=3/2ED \RightarrowMN=3/4BC
Đúng thì thanks giùm nha

tic mình nha!

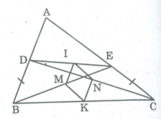
*Trong  ∆ BCD,ta có:

K là trung điểm của BC (gt)

N là trung điểm của CD (gt)

Nên NK là đường trung bình của  ∆ BCD

⇒ NK // BD và NK = 1/2 BD (1)

*Trong  ∆ BED,ta có:

M là trung điểm của BE (gt)

I là trung điểm của DE (gt)

Nên MI là đường trung bình của  ∆ BED

⇒ MI // BD và MI = 1/2 BD (t/chất đường trung bình trong tam giác) (2)

Từ (1) và (2) suy ra: MI // NK và MI = NK

Nên tứ giác MKNI là hình bình hành.

*Trong ∆ BEC ta có MK là đường trung bình.

⇒ MK = 1/2 CE (t/chất đường trung bình của tam giác)

BD = CE (gt). Suy ra: MK = KN

Vậy hình bình hành MKNI là hình thoi.

⇒IK ⊥ MN (t/chất hình thoi).