Question

Cho tam giác ABC. Lấy các điểm D,E theo thứ tự trên cạnh AB, AC sao cho BD = CE. Gọi M,N,I,K theo thứ tự là trung điểm của BE, CD, DE, BC. Chứng minh rằng IK vuông góc với MN.

Answer 1

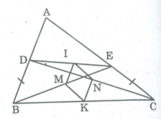
*Trong  ∆ BCD,ta có:

K là trung điểm của BC (gt)

N là trung điểm của CD (gt)

Nên NK là đường trung bình của  ∆ BCD

⇒ NK // BD và NK = 1/2 BD (1)

*Trong  ∆ BED,ta có:

M là trung điểm của BE (gt)

I là trung điểm của DE (gt)

Nên MI là đường trung bình của  ∆ BED

⇒ MI // BD và MI = 1/2 BD (t/chất đường trung bình trong tam giác) (2)

Từ (1) và (2) suy ra: MI // NK và MI = NK

Nên tứ giác MKNI là hình bình hành.

*Trong ∆ BEC ta có MK là đường trung bình.

⇒ MK = 1/2 CE (t/chất đường trung bình của tam giác)

BD = CE (gt). Suy ra: MK = KN

Vậy hình bình hành MKNI là hình thoi.

⇒IK ⊥ MN (t/chất hình thoi).