tìm 2 nguyên tố biết nguyến tố a và b biết : 2a3- b2 = 2( 4a - b)

Những câu hỏi liên quan
tìm số nguyên tố d để 4d^2+1 và 6d^2+1 lá số nguyên tố
Tìm số nguyên tố a,b để 4a+b và ab+11 là số nguyên tố
tìm a;b là số tự nhiên biết 4a^2+b^4 là số nguyên tố
Một nguyên tử X có tổng số hạt là 46 trong đó số hạt không mạng điện chiếm khoảng 34,8%
a/ Tính số hạt mỗi loại trong nguyên tử. Cho biết X là nguyên tử của nguyên tố nào?
b/ Vẽ sơ đồ cấu tạo nguyên tử của nguyến tố đó và cho biết nguyên tử đó có bao nhiêu lớp e, có bao nhiêu e lớp ngoài cùng.
a) Tổng số hạt là 46
=> 2Z + N= 46 (*)
Số hạt mang điện chiếm khoảng 34,8%
=> N=46.34,8%=16
Từ (*) => Z=15=P=E
Vì Z=15 => X là Phốt pho (P)
b) Cấu hình e : \(1s^22s^22p^63s^23p^3\)
Sơ đồ cấu tạo nguyên tử của nguyến tố Phốt pho
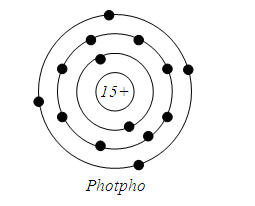
=> Có 3 lớp e, có 5e lớp ngoài cùng
Đúng 0
Bình luận (0)
B1:Cho p là số nguyên tố 3.Chứng minh rằng (p-1)(p+4) chia hết cho 6B2:Chứng minh rằng chỉ có duy nhất 1 bộ 3 số nguyên tố mà hiệu của 2 số liên tiếp 4B3:Tìm số nguyên tố 200, biết rằng khi chia nó cho 60 thì số dư là hợp số B4: Tìm các số nguyên tố a,b,c biết 2a+6b+21c78B5:Tìm 3 số nguyên tố liên tiếp a,b,c (abc) sao cho Aa^2+b^2+c^2 cũng là số nguyên tốGiúp mình với, mình sẽ tick cho
Đọc tiếp
B1:Cho p là số nguyên tố >3.Chứng minh rằng (p-1)(p+4) chia hết cho 6
B2:Chứng minh rằng chỉ có duy nhất 1 bộ 3 số nguyên tố mà hiệu của 2 số liên tiếp =4
B3:Tìm số nguyên tố <200, biết rằng khi chia nó cho 60 thì số dư là hợp số
B4: Tìm các số nguyên tố a,b,c biết 2a+6b+21c=78
B5:Tìm 3 số nguyên tố liên tiếp a,b,c (a<b<c) sao cho A=a^2+b^2+c^2 cũng là số nguyên tố
Giúp mình với, mình sẽ tick cho
B1: ƯCLN của 2 số là 45. Số lớn là 270,tìm số nhỏ.
B2: Tìm 2 số biết tổng của chúng là 162 và ƯCLN của chúng là 8.
B3: Tìm 2 số tự nhiên nhỏ hơn 200 biết hiệu của chúng là 90 và ƯCLN của chúng là 15.
B4: Tìm 2 số biết tích của chúng là 8748 và ƯCLN của chúng là 27.
B5: Chứng minh rằng: Nếu a và b là 2 số nguyên tố cùng nhau thì a và a+b là 2 số nguyên tố cùng nhau.
b2;
Goị hai số cần tìm là : a , b ( a> b )
Ta có :ƯCLN(a,b)=18
=>a=18m , b=18n mà ƯCLN(m,n)=1
=>a+b=18m+18n=18(m+m)=162
=> m+ n = 162:18=9
Ta có bảng sau :
| m | 1 | 8 | 2 | 7 | 4 | 5 |
| n | 8 | 1 | 7 | 2 | 5 | 4 |
| a | 18 | 144 | 36 | 126 | 72 | 90 |
| b | 144 | 18 | 126 | 36 | 90 | 72 |
Đúng 0
Bình luận (0)
b3:
Gọi hai số cần tìm là : a , b ( a >b )
Ta có : ƯCLN(a,b)=15
=> a = 15m , b = 15n mà ƯCLN(m,n)=1
=>a+b=15m-15n=15(m-n)=90
=>m+n=90:15=6
Vì : b < a < 200 nên n < m < 13
Bạn lập bảng tương tự như trên nhé nhớ ƯCLN(m,n)=1
xin lỗi tớ có việt gấp
Đúng 0
Bình luận (1)
Cho a;b;c là các số nguyên tố . Tìm a;b;c , biết :
a2 + b2 + c2 = 5070
Lời giải:
Không mất tổng quát giả sử $a\leq b\leq c$
Nếu $a,b,c$ đều là số nguyên tố lẻ thì $a^2+b^2+c^2$ là số lẻ. Mà $5070$ chẵn nên vô lý.
Do đó trong 3 số $a,b,c$ tồn tại ít nhất 1 số chẵn.
Số nguyên tố chẵn luôn là số bé nhất (2) nên $a=2$
Khi đó: $b^2+c^2=5070-a^2=5066\geq 2b^2$
$\Rightarrow b^2\leq 2533$
$\Rightarrow b< 51$
$\Rightarrow b\in \left\{2; 3; 5; 7; 11; 13; 17; 19; 23; 29; 31; 37; 41; 43; 47\right\}$
Thử các TH này ta thấy $(b,c)=(5,71), (29,65)$
Vậy $(a,b,c)=(2,5,71), (2,29,65)$ và các hoán vị.
Đúng 2
Bình luận (0)
vì 5070 là số chẵn ⇒ một trong 3 số a,b,c chẵn hoặc cả 3 số a,b,c chẵn
+) cả 3 số a,b,c chẵn
=> a=2, b=2, c=2 ( vì a,b,c là các số nguyên tố )
khi đó: a2+b2+c2= 12(loại)
=> một trong 3 số a,b,c chẵn
vì giá trị các số bằng nhau, giả sử a chẵn => a=2
khi đó: a2+b2+c2= 4+b2+c2
=> b2+c2= 5066
vì số chính phương có tận cùng là 0, 1, 4, 5, 6, 9 mà b2 và c2 là số chính phương có tận cùng là 0, 1, 4, 5, 6, 9
=> b2 và c2 có tận cùng là 0, 1, 4, 5, 6, 9
Mà b và c lẻ
=> b2 và c2 có tận cùng là 1, 5, 9
mà 5066 có tận cùng là 6
=> b2 và c2 có tận cùng là 1, 5
=> b và c có tận cùng là 1, 5
giả sử b có tận cùng là 5=> b=5
khi đó: 25+ c2 = 5066
c2 = 5041=712
=> c = 71
vậy, a=2, b=5, c=71 và các hoán vị của nó
Đúng 1
Bình luận (0)
Cho các nguyên tử sau: ![]() C , O , Mg , P , Ca , Ar , Ge , Br, Zn .
C , O , Mg , P , Ca , Ar , Ge , Br, Zn .
a) Hãy viết cấu hình electron nguyên tử của các nguyên tố
b) Cho biết nguyến tố nào là kim loại , nguyên tố nào là phi kim, nguyên tố nào là khí hiếm? Vì sao?
c) Cho biết nguyên tố nào thuộc nguyên tố s , p , d , f ?
a, Tìm số nguyên tố m, n biết : mn + 11 và 7m + n là các số nguyên tố
b, Tìm 3 SNT liên tiếp p,q,r biết p^2 + q^2 + r^2 là số nguyên tố.
Thay hướng dẫn tiếp phần b nhé:
Giả sử cả 3 số p;q;r đều không chia hết cho 3 thế thì p2;q2;r2 chia cho 3 chỉ dư 1 ( vì p;q;r nguyên tố)
Suy ra: p2 + q2 + r2 chia hết cho 3 mà p2 + q2 + r2 >3 suy ra p2 + q2 + r2 là hợp số ( mâu thuẫn đề bài).
Vậy điều giả sử là sai suy ra trong 3 số tồn tại ít nhất một số chia hết cho 3
Không mất tính tổng quat giả sử p<q<r\(\Rightarrow\)p chia hết cho 3 mà p là số nguyên tố suy ra p = 3
Lại có: p;q;r là 3 số nguyên tố liên tiếp nên q = 5; r=7
Vậy (p;q;r) = (3;5;7) và các hoán vị
Đúng 1
Bình luận (0)
b, Giả sử 3 số nguyên tố p, q, r đều không chia hết cho 3 mà một số chính phương chia hết cho 3 hoặc chia 3 dư 1
Nếu p^2, q^2, r^2 chia hết cho 3 suy ra p^2 + q^2 + r^2 chia hết cho 3 ( là hợp số, loại )
Nếu p^2, q^2, r^2 cùng chia 3 dư 1 suy ra p^2 + q^2 + r^2 chia hết cho 3 ( loại )
Nếu trong 3 số có 1 số chia hết cho 3 suy ra p^2 + q^2 + r^2 chia 3 dư 2 ( 2 số còn lại chia 3 dư 1 ) loại vì không có số chính phương nào chia 3 dư 2
Nếu trong 3 số có 1 số chia 3 dư 1 thì p^2 + q^2 + r^2 chia 3 dư 1 ( 2 số còn lại chia hết cho 3 ) chọn
Vậy trong 3 số p , q , r phải có ít nhất 1 số chia hết cho 3
mà p, q, r là các số nguyên tố nên có 1 số nhận giá trị là 3.
Do 1 ko là số nguyên tố nên bộ ba số nguyên tố có thể là 2 - 3 - 5 hoặc 3 - 5 - 7
Với 3 số nguyên tố là 2 - 3 - 5 thì p^2 + q^2 + r^2 = 2^2 + 3^2 + 5^2 = 38 ( là hợp số, loại )
Vậy 3 số nguyên tố cần tìm là 3 5 7
Nguyễn Vân Huyền đã chọn câu trả lời này
Đúng 0
Bình luận (0)
Vai trò của p,q,rp,q,r là như nhau nên giả sử p>q>rp>q>r
Xét p=2p=2,ta tìm được 3 số là 2;3;5.Không thỏa
Xét p=3p=3,ta tìm được 3 số là 3;5;7 thỏa
Xét p>3p>3
Bổ đề:Mọi số nguyên tố >3>3 nến đem bình phương lên thì luôn chia 3 dư 1
thật vậy các số nguyên tố lớn hơn 3 nện có dạng 3k+13k+1 hoặc 3k+23k+2
Nếu có dạng 3k+13k+1,ta có:(3k+1)2=9k2+6k+1≡1(mod3)(3k+1)2=9k2+6k+1≡1(mod3)
Nếu có dạng 3k+23k+2,ta có (3k+2)2=9k2+12k+4≡1(mod3)(3k+2)2=9k2+12k+4≡1(mod3)
Vậy nếu p>3p>3 thì các số q,r>3q,r>3nên khi bình phương lên đều dư 1
⇒p2+q2+r2≡0(mod3)⇒p2+q2+r2≡0(mod3)
Vậy ta có (3;5;7)(3;5;7) và các hoán vị
Đúng 0
Bình luận (0)
1, Tìm 2 số nguyên tố p, biết p^2+14 là số nguyên tố
2, tìm số nguyên dương a,b,x, biết
x+3=2^a và 3x+1 = 4b
1:đáp án là 3
2:đáp án lần lượt là
x = 5
a = 3
b = 4
Đúng 0
Bình luận (0)
Tìm 2 số nguyên tố a và b thoả mãn 4a + 7b = 49




















