Chọn D.

Mỗi câu hỏi có 4 phương án trả lời nên số cách chọn phương án trả lời cho 5 câu hỏi vận dụng cao là n Ω = 4 . 4 . 4 . 4 . 4 = 4 5  

Vì mỗi câu hỏi có 3 phương án trả lời sai nên số cách chọn để học sinh đó trả lời sai cả 5 câu hỏi vận dụng cao là n A = 3 . 3 . 3 . 3 . 3 = 243  

Xác suất cần tìm là P A = n A n Ω = 243 4 5  

Đáp án A

Thí sinh thi được 26 điểm do đó có 6 phương án đúng và 4 phương án sai

Xác suất cần tìm sẽ là:

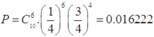
=>  Chọn phương án A.

Chú ý: Công thức tổng quát cho bài toán n câu hỏi và a đáp án đúng sẽ là

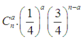
CHỊUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUU

Đáp án A

Thí sinh thi được 26 điểm do đó có 6 phương án đúng và 4 phương án sai

Xác suất cần tìm sẽ là:

  P = C 10 6 1 4 6 3 4 4 = 0 . 016222

Chọn phương án A.

Chú ý: Công thức tổng quát cho bài toán n câu hỏi và a đáp án đúng sẽ là  C n a 1 4 a 3 4 n - a

Đù mé bài này mà của bọn mẫu giáo 😑😑

Đáp án B

Giả sử để đạt được 26 điểm thì số câu chọn đúng là a, sai là 10-a.

Ta có: 5a-1(10-a) = 26 => 6a = 36 => a = 6.

Vậy phải chọn được 6 câu đúng và 4 câu sai.

Xác suất chọn 1 câu được đúng là:

Xác suất chọn 1 câu được sai là:

Có cách chọn 6 câu đúng, 4 câu sai.

Vậy xác suất để được 26 điểm là: 

Chọn C (vì nước sôi ở  100 o C ).

Giải:

Vì mỗi thí sinh phải giải 5 bài toán. Mỗi bài toán đúng được tính 4 điểm. Mỗi bài toán sai hoặc không làm được đều bị trừ 2 điểm nên ta có 5 trường hợp sau:

Nếu đúng 5 bài thì số điểm được là: 5. 4 = 20 (điểm).

Nếu đúng 4 bài thì số điểm được là: 4. 4 - 2 = 14 (điểm).

Nếu đúng 3 bài thì số điểm được là: 3. 4 – 4 = 8 (điểm).

Nếu đúng 2 bài thì số điểm được là: 2. 4 – 6 = 2 (điểm).

Nếu đúng 1 bài hoặc không đúng bài nào thì đều được 0 điểm.

Như vậy có 6 thí sinh dự thi nhưng chỉ có 5 loại điểm nên theo nguyên lý Điricle sẽ có ít nhất 2 thí sinh bằng điểm nhau.

Bố con hâm vừa hỏi vừa trả lời 

Tớ làm giống cậu

Đúng 100%

Đúng 100%

Đúng 100%

Phương án D.

Có thể hoàn chỉnh lại :

- Ý 1 : Nước cất là tinh khiết

- Hoặc sửa lại ý 2 : Vì nước cất tạo bởi hai nguyên tố hidro và oxi