cho 1 hình chữ nhật có diện tích là 240m2
nếu tăng chiều rộng lên 3m và giảm chiều dài đi 4m
thì diện tích không đổi
tính chu vi của hình chữ nhật ban đầu ?
Một hình chữ nhật co diện tích la 240m2 .Nếu tăng chiều rộng len 3m và giảm chiều dài 4m thì diện tích không đổi .Tính chu vi hcn ban đầu
Gọi chiều dài của hình chữ nhật là : x (m , x>4 )
Chiều rộng của hình chữ nhật là : 240 / x (m)
Chiều dài khi đó là : x - 4 (m)
Chiều rộng khi đó là : 240/x +3 (m)
Khi đó diện tích của hình chữ nhật không đổi nên ta có phương trình : (x - 4)(240/x +3) = 240
=> x = 20 (thỏa mãn ) hoặc x = -16 (loại )
Vậy chiều dài hình chữ nhật là 20 m
chiều rộng hình chữ nhật là 12 m
Một hình chữ nhật có chiều dài hơn chiều rộng 4m. Nếu tăng chiều rộng lên 2m và giảm chiều dài đi 3m thì chu vi của hình chữ nhật đó giảm đi 2m. Tính diện tích hình chữ nhật ban đầu.
Một mảnh đất hình chữ nhật có diện tích 240 m 2 . Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì diện tích mảnh đất không đổi. Tính kích thước của mảnh đất.
Gọi chiều rộng của mảnh đất là x (m, x > 0).
Diện tích bằng
240
m
2
⇒
Δ
=
3
2
–
4
.
1
.
(
-
180
)
=
729
⇒ Chiều dài mảnh đất là: 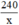 (m).
(m).
Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:
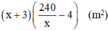
Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:
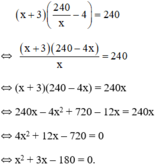
Có a = 1; b = 3; c = -180
Phương trình có hai nghiệm:
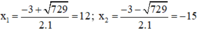
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).
Bài 6. Một hình chữ nhật nếu tăng chiều rộng thêm 6m thì diện tích tăng 240m2
. Nếu tăng
chiều rộng thêm 4m và giảm chiều dài đi 4m thì diện tích tăng 24m2
. Tính diện tích hình chữ
nhật ban đầu
Ta có
S = a.b
S mới
=>a . ( b + 6 ) = S + 240 m2
=> a.b + a.6 = S + 240 m2
Ta lấy S mới trừ đi S cũ đc a . 6 = 240 m2 => a = 40 m
Mặt khác nếu
( a - 4 ) . ( b + 4 ) = S + 24m2
(40 - 4 ) . ( b + 4 ) = S + 24 m2
=> 36 . ( b + 4 ) = S + 24m2
=> 36 . b + 36 . 4 = S + 24m2
=> 36.b + 144 = S + 24m2
=> S = 36 . b + ( 144- 24 )
=> S = 36. b + 120 = 40 . b
=> 36. b + 120 = 40 . b
=> 120 = 4b
=> b = 30 => S = 40 . 30 = 1200 m2
Một mảnh đất hình chữ nhật có diện tích 240m2. Nếu tăng chiều rộng 3m và giảm chiều dài 4m thì diện tích mảnh đất không đổi. Tính kích thước của mảnh đất
Gọi chiều dài của mảnh đất hình chữ nhật là x (m, x > 4)
Khi đó chiều rộng của mảnh đất hình chữ nhật là \(\frac{240}{x}\left(m\right)\)
Khi tăng chiều rộng 3m, giảm chiều dài 4m thì diện tích mảnh đất là:
\(\left(x-4\right)\left(\frac{240}{x}+3\right)\)
Do diện tích không đổi nên ta có phương trình:
\(\left(x-4\right)\left(\frac{240}{x}+3\right)=240\)
\(\Rightarrow240+3x-\frac{960}{x}-12=240\)
\(\Rightarrow3x^2-12x-960=0\Rightarrow\orbr{\begin{cases}x=20\left(n\right)\\x=-16\left(l\right)\end{cases}}\)
Vậy chiều dài mảnh đất là 20m, chiều rộng mảnh đất là 12m.
hình chữ nhật có chiều dài gấp đôi chiều rộng nếu tăng chiều rộng lên 1m ,giảm chiều dài 1m thì diện tích tăng 3m vuông tính chu vi của hình chữ nhật ban đầu .
Gọi chiều rộng là x
Chiều dài là 2x
Theo đề, ta có: (x+1)(2x-1)=2x2+3
\(\Leftrightarrow2x^2-x+2x-1=2x^2+3\)
=>x-1=3
hay x=4
Vậy: Chu vi là 24m
Một hình chữ nhật có chu vi là 18 cm, khi giảm chiều dài đi 20% chiều dài ban đầu và tăng chiều rộng thêm 25% chiều rộng ban đầu thì chu vi hình chữ nhật không đổi. Tính diện tích hình chữ nhật.
Một hình chữ nhật có chu vi là 26 m . Nếu bớt chiều dài đi 3m và tăng chiều rộng thêm 2m thì diện tích vẫn không thay đổi . Tính diện tích hình chữ nhật ban đầu
Tính chu vi của một hình chữ nhật , biết rằng nếu tăng mỗi chiều hình chữ nhật lên 5 m thì diện tích hình chữ nhật tăng 225 m2. Nếu tăng chiều rộng lên 2 m và giảm chiều dài đi 5 m thì diện tích hình chữ nhật bằng diện tích ban đầu.
Gọi a là chiều dài, b là chiều rộng (a, b m; a> b > 0)
Diện tích HCN là S= ab
Nếu tăng mỗi cạnh lên 5m thì S tăng 225 m2m2
=> (a+5)(b+5)= ab+ 225
<=> ab+ 5a+ 5b+ 25= ab+ 225
<=> a+b= 40 (1)
Nếu tăng chiều rộng 2m, giảm chiều dài 5m thì S không đổi
=> (a-5)(b+2)= ab
<=> ab+ 2a - 5b -10= ab
<=> 2a - 5b= 10 (2)
(1)(2) => a= 30; b= 10 (TM)
Vậy chu vi HCN là (30+10).2= 80m