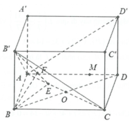
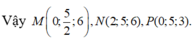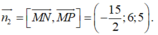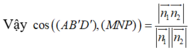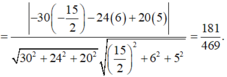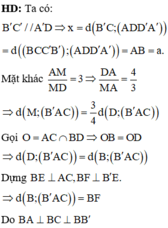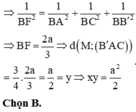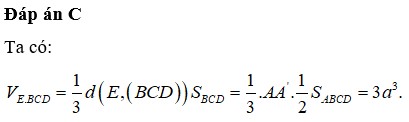Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=2, AD=4, AA'=5. Gọi M là trung điểm A'D'. Tính |2BM+DA|

Những câu hỏi liên quan
Cho hình hộp chữ nhật ABCD.ABCD có AB4 AD 5 AA6 . Gọi M , N , P lần luợt là trung điểm các cạnh AD, CD và DD (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (ABD) và bằng (MNP) A.
181
469
B.
120
13
469
C.
19
469...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=4 AD =5 AA'=6 . Gọi M , N , P lần luợt là trung điểm các cạnh A'D', C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và bằng (MNP)
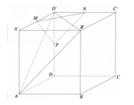
A. 181 469
B. 120 13 469
C. 19 469
D. 60 61 469
Cho hình hộp chữ nhật ABCD.ABCD có AB 4, AD 5, AA 6. Gọi M, N, P lần lượt là trung điểm các cạnh AD, CD và DD (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (ABD) và (MNP) bằng A.
181
469
B.
120
13
469
C.
19
469...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB =4, AD = 5, AA' =6. Gọi M, N, P lần lượt là trung điểm các cạnh A'D', C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và (MNP) bằng
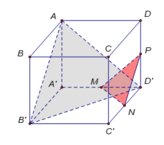
A. 181 469
B. 120 13 469
C. 19 469
D. 60 61 469
Chọn A
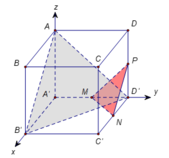
Đối với những bài cồng kềnh và tính toán rất phức tạp
thế này thì nên tọa độ hóa giải rất nhanh, khỏi phải mất nhiều
thời gian và tư duy. Gắn trục tọa độ Oxyz như hình vẽ bên với
A'(0;0;0), D(0;5;6), C' (4;5;0)
![]()
![]()
![]()
![]()
![]()
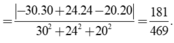
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có AB4,AD5,AA6. Gọi M , N , P lần luợt là trung điểm các cạnh AD,CD và DD (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (ABD) và (MNP) bằng A.
181
469
B.
120
13
469
C.
19
469
D.
60
61
469
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=4,AD=5,AA'=6. Gọi M , N , P lần luợt là trung điểm các cạnh A'D',C'D' và DD' (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (AB'D') và (MNP) bằng
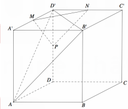
A. 181 469
B. 120 13 469
C. 19 469
D. 60 61 469
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
2
a
,
A
A
a
. Gọi M là điểm trên đoạn AD với
A
M
M
D...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = 2 a , A A ' = a . Gọi M là điểm trên đoạn AD với A M M D = 3 . Gọi x là độ dài khoảng cách giữa hai đường thẳng A'D, B'C và y là độ dài khoảng cách từ M đến mặt phẳng (AB'C). Tính giá trị xy.
A. 5 a 2 3
B. a 2 2
C. 3 a 2 4
D. 3 a 2 2
Cho hình hộp chữ nhật ABCD.ABCD. Gọi M, N lần luợt là trung điểm BD và BDa) Nêu vị trí tương đối của các cặp đường thẳng MN và BD; MNvà CC; AC và AD.b) Chứng minh MN ^ (ABCD).c) Biết AA 20 cm,AB 30 cm,AD 40 cm. Tính BD; BM.d) Tính thể tích hình hộp
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Gọi M, N lần luợt là trung điểm BD và B'D'
a) Nêu vị trí tương đối của các cặp đường thẳng MN và BD; MNvà CC'; AC và A'D'.
b) Chứng minh MN ^ (A'B'C'D').
c) Biết AA' = 20 cm,AB = 30 cm,AD = 40 cm. Tính B'D'; B'M.
d) Tính thể tích hình hộp
a) Ta có MN cắt BD tại M.
MN//CC', AC và A'D' chéo nhau.
b) MN ^ A'C' và B'D'
c) B'S' = 50cm, B'M = 5 41 c m
d) V =24000cm3
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
2
a
,
A
D
a
,
A
A
a
3
. Gọi M là trung điểm cạnh AB. Khoảng cách từ D đến mặt phẳng (BMC) bằn...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = 2 a , A D = a , A A ' = a 3 . Gọi M là trung điểm cạnh AB. Khoảng cách từ D đến mặt phẳng (B'MC) bằng
A. a 21 7
B. 2 a 21 7
C. 3 a 21 7
D. a 21 14
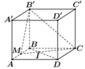
Khoảng cách từ D đến (B'MC)
gấp hai lần khoảng cách từ B đến (B'MC)
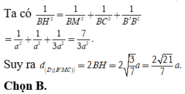
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có AA 2a, AD 4a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M A.
d
2
a
2
B.
d
a
2
C.
d
2
a
D.
d
3
a
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = 2a, AD = 4a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M
A. d = 2 a 2
B. d = a 2
C. d = 2 a
D. d = 3 a
Đáp án A
Chọn hệ trục tọa độ như hình vẽ
A'(0;0;0), B'(4a;0;0), C'(4a;4a;0), M'(0;2a;2a)
A ' B ' → 4 a ; 0 ; 0 , C ' M → - 4 a ; - 2 a ; 2 a ⇒ A ' B ' → , C ' M → = 0 ; - 8 a 2 ; - 8 a 2 A ' M → 0 ; 2 a ; 2 a d ( A ' B ' , C ' M ) = A ' B ' → , C ' M → A ' M A ' B ' → , C ' M → = 32 a 3 8 2 a 2 = 2 2 a
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có AA 2a, AD 4a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M. A.
d
2
a
2
B.
d
a
2
C. d 2a D. d 3a
Đọc tiếp
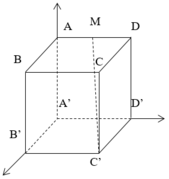
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = 2a, AD = 4a. Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M.
A. d = 2 a 2
B. d = a 2
C. d = 2a
D. d = 3a
Đáp án A
Chọn hệ trục tọa độ như hình vẽ
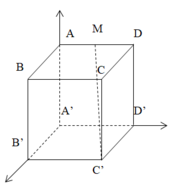
A ' ( 0 ; 0 ; 0 ) , B ' ( 4 a ; 0 ; 0 ) , C ' ( 4 a ; 4 a ; 0 ) , M ( 0 ; 2 a ; 2 a ) A ' B ' → ( 4 a ; 0 ; 0 ) , C ' M → ( − 4 a ; − 2 a ; 2 a ) ⇒ [ A ' B ' → , C ' M → ] = ( 0 ; − 8 a 2 ; − 8 a 2 ) A ' M → ( 0 ; 2 a ; 2 a ) d ( A ' B ' , C ' M ) = [ A ' B ' → , C ' M → ] A ' M → [ A ' B ' → , C ' M → ] = 32 a 3 8 2 a 2 = 2 2 a
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có AB2a, AD3a, AA3a. Gọi E là trung điểm BC. Thể tích khối chóp E.BCD bằng A.
a
3
2
B.
a
3
C.
3
a
3
D.
4
a...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=2a, AD=3a, AA'=3a. Gọi E là trung điểm B'C'. Thể tích khối chóp E.BCD bằng
A. a 3 2
B. a 3
C. 3 a 3
D. 4 a 3 3
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
2
a
,
A
D...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = 2 a , A D = 3 a , A A ' = 3 a . Gọi E là trung điểm B ' C ' . Thể tích khối chóp E.BCD bằng
A. a 3 2
B. a 3
C. 3 a 3
D. 4 a 3 3
Đáp án C
Ta có:
V E . B C D = 1 3 d ( E , ( B C D ) ) S B C D = 3 a 3
Đúng 0
Bình luận (0)