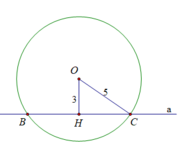
Khung thép của một phần sân khấu có dạng đường tròn bán kính 15m. Mắt của một người thợ ở vị trí A nhìn hai đèn ở các vị trí B, C (A, B, C cùng thuộc đường tròn bán kính 15m), bằng cách nào đó, người thợ thấy rằng góc nhìn \(\widehat {BAC} = 30^\circ \) (hình 31). Khoảng cách giữa hai vị trí B và C bằng bao nhiêu mét?