Một mặt phẳng đi qua tâm hình cầu, cắt hình cầu theo một hình tròn có diện tích 9π cm2. Thể tích của hình cầu bằng
A. 972π cm3. B. 36π cm3.
C. 6π cm3. D. 81π cm3.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3. Mặt phẳng ( α ) qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP.
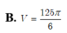


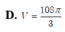
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA = 3. Mặt phẳng ( α ) qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP.
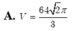
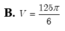
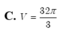
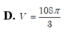
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2 2 , cạnh bên SA vuông góc với mặt phẳng đáy và SA=3 Mặt phẳng α qua A và vuông góc với SC cắt các cạnh SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tự diện CMNP.
A. V = 64 2 π 3
B. V = 125 π 6
C. V = 32 π 3
D. V = 10 Sπ 3
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng
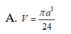
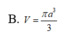
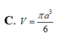
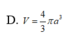
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng
A. V = πa 3 24
B. V = πa 3 3
C. V = πa 3 6
D. V = 4 3 πa 3
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là V. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên).
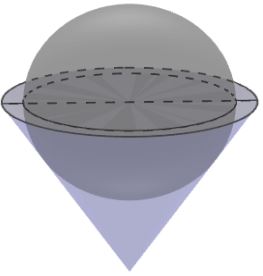
Tính thể tích nước còn lại trong bình.
A. 1 6 V
B. 1 3 V .
C. V
D. 1 π V .
Đáp án B
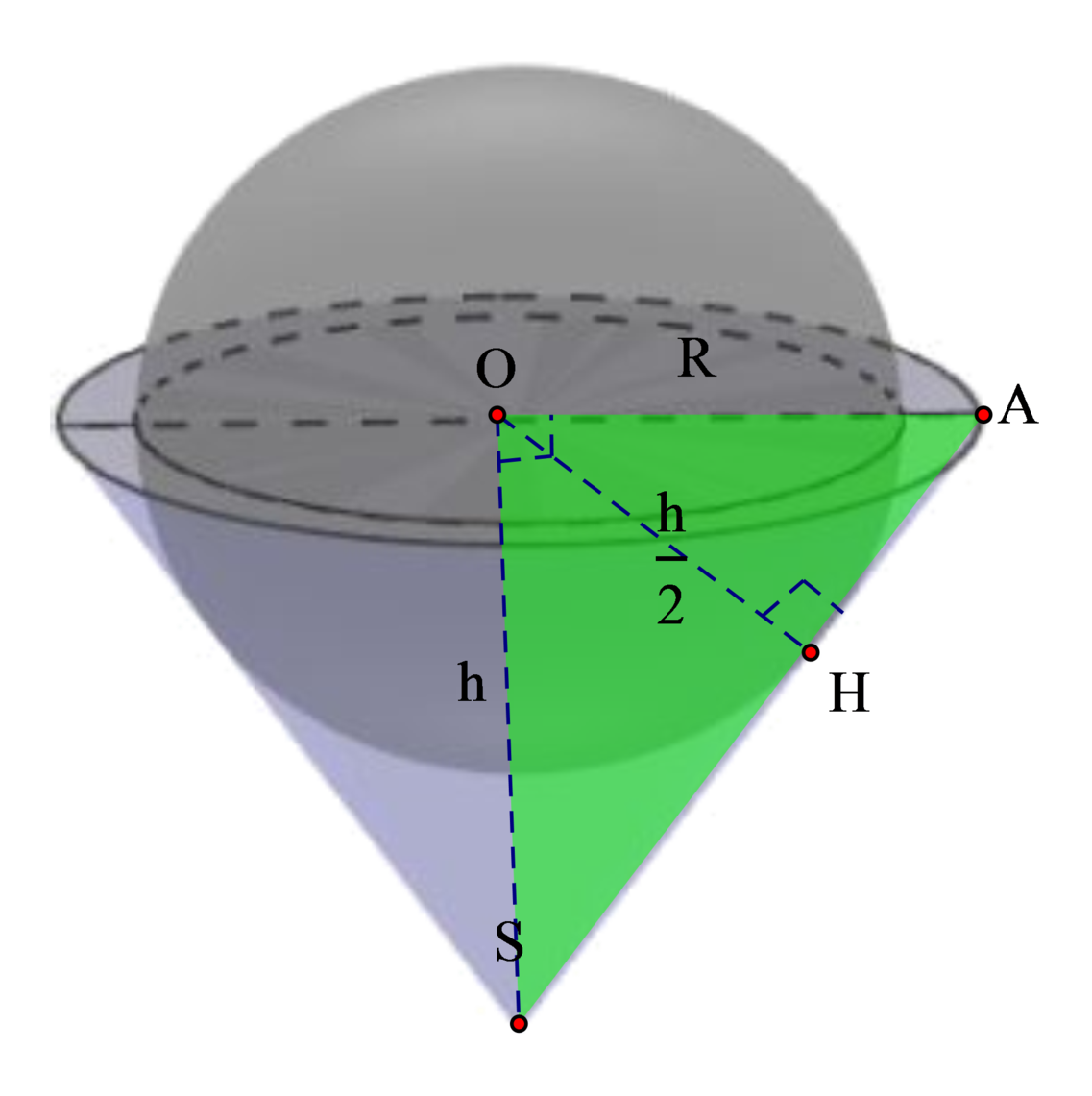
Thể tích nước tràn ra là 1 2 thể tích quả cầu
⇒ V = 1 2 4 3 π h 2 3 = π h 3 12 ⇒ π h 3 = 12 V
Gọi R là bán kính đáy hình nón. Áp dụng hệ thức lượng trong tam giác vuông SOA ta có:
1 O H 2 = 1 S O 2 + 1 O A 2 ⇔ 4 h 2 = 1 h 2 + 1 R 2 ⇒ R = h 3
từ đây ta tính được thể tích hình nón là:
V n = 1 3 π R 2 h = 1 3 π h 2 3 h = π h 3 9 = 12 V 9 = 4 3 V
Vậy thể tích nước còn lại là:
V = 4 3 V − V = V 3 .
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là V. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Tính thể tích nước còn lại trong bình.
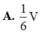
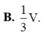
![]()
![]()
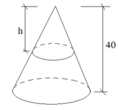
Một vật N 1 có dạng hình nón có chiều cao bằng 40cm. Người ta cắt vật N 1 bằng một mặt phẳng song song với mặt đáy của nó để được một hình nón nhỏ N 2 có thể tích bằng 1 8 thể tích N 1 . Tính chiều cao h của hình nón N 2 ?
![]()
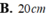
![]()
![]()
Một hình lập phương có thể tích là 125m3. Một hình hộp chữ nhật có diện tích đáy bằng diện tích một mặt của hình lập phương đó và chiều cao là 3m. Tính thể tích của hình chữ nhật đó
Ta có:125m3=5cmx5cmx5cm
Vậy độ dài một cạnh hình lập phương là 5cm
Diện tích một mặt của hình lập phương là:5x5=25(cm2)
Ta có:25cm2=2,5cmx10cm
Vậy chiều dài của hình hộp chữ nhật là 10cm;chiều rộng của hình hộp chữ nhật là 2,5cm
Thể tích của hình hộp chữ nhật đó là:10x3x2,5=75(cm3)
Đáp số:75cm3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.
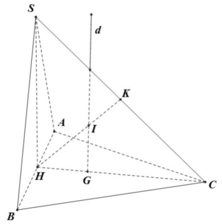
A. 5 π 15 18
B. 5 π 15 54
C. 4 π 3 27
D. 5 π 3