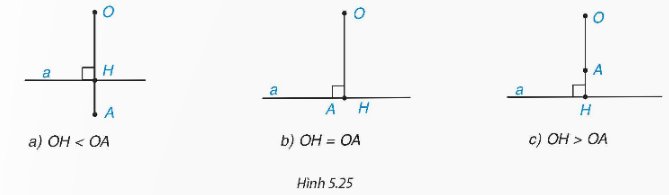
Cho đường thẳng a và điểm O. Gọi H là chân đường vuông góc hạ từ O xuống a, và A là một điểm thuộc tia OH. Trong mỗi trường hợp sau đây, hãy vẽ đường tròn (O; OA) và cho biết đường thẳng a và đường tròn (O; OA) có bao nhiêu điểm chung?
cho đường tròn (O) đường kính AB. trên tia AB lấy điểm D nằm ngoài đoạn thẳng AB và kẻ tiếp tuyến DC với đường tròn (O) ( C là tiếp điểm) . gọi E là chab đường vuông góc hạ từ A xuống đường thẳng CD và F là chân đường vuông góc hạ từ D xuống đường thẳng AC . chứng minh tứ giác EFDA nội tiếp
Cho đường tròn tâm O và dây cung BC không đi qua O. Một điểm A chuyển động trên dường tròn (A khác B, C). Gọi M là trung điểm của đoạn AC, H là chân đường vuông góc hạ từ M xuống đường thẳng AB. Chứng minh rằng H nằm trên một đường tròn cố định.
: Cho nửa đường tròn (O) đường kính AB và một điểm M nằm trên nửa đường tròn đó. H là chân đường vuông góc hạ từ M xuống AB. a. Khi AH=2cm, MH=4cm. Hãy tính độ dài các đoạn thẳng: AB, MA, MB.
b. Khi điểm M di động trên nửa đường tròn (O). Hãy xác định vị trí của M để biểu thức: có giá trị nhỏ nhất.
c. Tiếp tuyến của (O) tại M cắt tiếp tuyến của (O) tại A ở D, OD cắt AM tại I. Khi điểm M di động trên nửa đường tròn (O) thì I chạy trên đường nào ?
a/
Ta có \(\widehat{AMB}=90^o\) (góc nt chắn nửa đường tròn)
Xét tg vuông AMB có
\(MH^2=AH.BH\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền = tích giữa các hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow BH=\dfrac{MH^2}{AH}=\dfrac{4^2}{2}=8cm\)
\(\Rightarrow AB=AH+BH=2+8=10cm\)
\(MA^2=AH.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow MA=\sqrt{AH.AB}=\sqrt{2.10}=2\sqrt{5}cm\)
\(MB^2=BH.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow MB=\sqrt{BH.AB}=\sqrt{8.10}=4\sqrt{5}cm\)
b/ Không rõ bạn hỏi biểu thức nào?
c/
Ta có \(OD\perp AM\) (2 tiếp tuyến cùng xuất phát từ 1 điểm ngoài hình tròn thì đường nối điểm đó với tâm đường tròn vuông góc với dây cung nối 2 tiếp điểm)
Xét tg vuông AIO
Gọi K là trung điểm của AO => AK=OK
\(\Rightarrow IK=AK=OK=\dfrac{1}{2}AO\) không đổi (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Ta có
A; O cố định => K cố định; IK không đổi => khi M di chuyển trên nửa (O) => I chạy trên nửa đường tròn tâm K
Cho đường tròn (O) đường kính AB. Trên tia AB lấy điểm D nằm ngoài đoạn AB và kẻ tiếp tuyến DC với đường tròn (O) (C là tiếp điểm). Gọi E là chân đường vuông góc hạ từ A xuống đường thẳng CD và F là chân đường vuông góc hạ từ D xuống đường thẳng AC. Chứng minh:
a) Tứ giác EFDA nội tiếp.
b) AF là phân giác của .
c) Tam giác EFA và tam giác BDC đồng dạng.
d) Các tam giác ACD và ABF có cùng diện tích.
a) có 2 góc vg cùng nhìn 1 cạnh
b)EAC=ACO
tam giác AOC cân tại O
=>.......................
c) theo câu a =>AFE=ADE
từ câu b =>CAB=CAE
CAB=BCD
=>...........................
d) đang suy nghĩ
Cho nửa đường tròn tâm O đường kính BC=2R, A là một điểm bất kìa trên nửa đường tròn khác B và C. Kẻ AH vuống góc với BC, gọi E và F là chân đường vuông góc hạ từ H xuống AB và AC.
a) Cm AE.AB=AF.AC và EF^3=BE.CF.BC
b) Gọi I là điểm đối xứng của H qua AB. Cm IA là tiếp tuyến của nửa đường tròn.
c) Tìm vị trí của A để diện tích tam giác AHB lớn nhất.
Dạ em chỉ cần câu c thôi ạ, em cảm ơn ạ.
Cho nửa đường tròn (O) đường kính AB và một điểm M nằm trên
nửa đường tròn đó. H là chân đường vuông góc hạ từ M xuống AB.
a/ Khi AH=2cm, MH=4cm. Hãy tính độ dài các đoạn thẳng: AB,MA, MB.
b/ Khi điểm M di động trên nửa đường tròn (O). Hãy xác định vị trí của M để biểu thức:
\(\frac{1}{MA^2}+\frac{1}{MB^2}\)có giá trị nhỏ nhất
a) MA=AH2+MH2−−−−−−−−−−−√=25–√MA=AH2+MH2=25
M∈(O)M∈(O) đk AB⇒AMBˆ=90∘⇒AMBAB⇒AMB^=90∘⇒AMB vuông tại M,MH⊥AB⇒AM2=AH.AB⇒AB=10M,MH⊥AB⇒AM2=AH.AB⇒AB=10
⇒MB=AB2−AM2−−−−−−−−−−√=45–√⇒MB=AB2−AM2=45
b) ⇒1MA2+1MB2⇒1MA2+1MB2 nhỏ nhất
Cho (O;R) và một cát tuyến d không đi qua tâm O. Từ một điểm M trên d và ở ngoài (O) ta kẻ hai tiếp tuyến MA và MB với đường tròn; BO kéo dài cắt (O) tại điểm thứ hai là C. Gọi H là chân đường vuông góc hạ từ O xuống d. Đường thẳng vuông góc với BC tại O cắt AM tại D.
1. CM: A;O;H;M;B cùng nằm trên 1 đường tròn.
2. CM: AC song song MO và MD=OD
3. Đường thẳng OM cắt (O) tại E và F . Chứng tỏ MA^2 = ME.MF
4. Xác định vị trí của điểm M trên d để tam giác MAB là tam giác đều. Tính diện tích phần tạo bởi hai tiếp tuyến với đường tròn trong trường hợp này.
Cho tam giác ABC có 3 góc nhọn nối tiếp trong đường tròn (O;R). Vẽ đường cao AH của tam giác ABC, đường kính AD của đường tròn. GỌi E, F lần lượt là chân đường vuông góc kẻ từ C và B xuống đường thẳng AD. M là trung điểm của BC.
a). Chứng minh các điểm A, B, H, F cùng thuộc một đường tròn; B, M, F, O cùng thuộc một đường tròn.
b) Chứng minh HE // BD
c) Khi OM = R/2, hãy tính diện tích hình quạt tròn được giới hạn bởi OB, OC và cung nhỏ BC
Cho đường tròn (O;R), đường kính MN. Lấy điểm A thuộc đường tròn (O;R) sao cho MA=R. Kẻ OH vuông góc với MA tại H. Qua điểm A vẽ một tiếp tuyến của đường tròn (O;R), tiếp tuyến này cắt đường thẳng OH tại C. Gọi D là điểm thuộc tia đối của tia AM. Chứng minh rằng : DA.DM = DO2 – OM2
https://www.youtube.com/channel/UCU_DXbWfhapaSkAR7XsK5yQ?view_as=subscriber

Gọi OD cắt (O) tại E,F \(\left(E\in DF\right)\)ta có:
\(\widehat{DAE}=\widehat{DFM}\)(cùng bù với \(\widehat{MAE}\))
\(\widehat{ADE}=\widehat{FDM}\)(chung)
Do đó \(\Delta DAE\text{~}\Delta DFM\text{ }\left(g.g\right)\)
\(\Rightarrow\frac{DA}{DF}=\frac{DE}{DM}\)
\(\Rightarrow DA.DM=DE.DF\)
\(=\left(DO-OE\right)\left(DO+OF\right)=\left(DO-OM\right)\left(DO+OM\right)=DO^2-OM^2\)(đpcm)
cho 4 điểm A, B, C, D nằm trên một đường tròn (O) sao cho AB là đường kính, còn C và D nằm khác phía so với AB. Gọi I và K là chân các đường vuông góc hạ từ A và B xuống đường thẳng CD. Chứng minh CI = DK