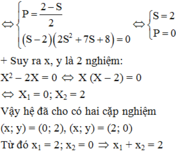Tìm nghiệm nguyên dương của phương trình : x2 + 2xy -y3=2013

Những câu hỏi liên quan
Bài 1 : tìm x ; y nguyên dương
2xy + x + y = 83
Bài 2 tìm nghiệm nguyên của phương trình :
a ) x2 + 2y2 + 3xy - x - y + 3 = 0
b ) 6x2y3 + 3x2 - 10y3 = -2
bài 1
Ta có 2xy+x+y=83
<=>4xy+2x+2y=166
2x*(2y+1)+(2y+1)=167
(2x+1)*(2y+1)=167
=>2x+1;2y+1 thuộc Ư(167)
do x,y nguyên dương =>2TH
TH1 2x+1=1;2y+1=167=>x=...;y=....
TH2 2x+1=167;2y+1=1=>x=...;y=....
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên dương của hệ phương trình:
x
+
y
z
x
3
+
y
3
z
2
Đọc tiếp
Tìm nghiệm nguyên dương của hệ phương trình: x + y = z x 3 + y 3 = z 2
Ta có: x 3 + y 3 = ( x + y ) 2 < = > ( x + y ) ( x 2 − x y + y 2 − x − y ) = 0
Vì x, y nguyên dương nên x+y > 0, ta có: x 2 − x y + y 2 − x − y = 0
⇔ 2 ( x 2 − x y + y 2 − x − y ) = 0 ⇔ x - y 2 + x - 1 2 + ( y - 1 ) 2 = 2
Vì x, y nguyên nên có 3 trường hợp:
+ Trường hợp 1: x − y = 0 x - 1 2 = 1 ⇔ x = y = 2 , z = 4 y - 1 2 = 1
+ Trường hợp 2: x − 1 = 0 x - y 2 = 1 ⇔ x = 1 , y = 2 , z = 3 y - 1 2 = 1
+ Trường hợp 3: y − 1 = 0 x - y 2 = 1 x - 1 2 = 1 ⇔ x = 2 , y = 1 , z = 3
Vậy hệ có 3 nghiệm (1,2,3);(2,1,3);(2,2,4)
Đúng 0
Bình luận (0)
Biết hệ phương trình
x
3
+
y
3
8
x
+
y
+
2
x
y...
Đọc tiếp
Biết hệ phương trình x 3 + y 3 = 8 x + y + 2 x y = 2 có hai nghiệm ( x 1 ; y 1 ) ; ( x 2 ; y 2 ) . Tổng x 1 + x 2 bằng?
A. 2
B. −2
C. 1
D. 0
tìm nghiệm nguyên dương của phương trình 7(x+1)+3y=2xy
phân tích pt ta được: \(\left(2x-3\right)\left(7-2y\right)=-35\)
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên của phương trình: x2 + 4y2 - 2xy 13 Ai giúp mình với ạ
Đọc tiếp
Tìm nghiệm nguyên của phương trình: x2 + 4y2 - 2xy = 13 Ai giúp mình với ạ
Lời giải:
$x^2+4y^2-2xy=13$
$\Leftrightarrow (x^2+y^2-2xy)+3y^2=13$
$\Leftrightarrow (x-y)^2+3y^2=13$
$\Rightarrow 3y^2=13-(x-y)^2\leq 13< 15$
$\Rightarrow y^2< 5$
Vì $y^2\geq 0$ với mọi $y$ nguyên nên $y^2\in\left\{0; 1;4\right\}$
Với $y^2=0$:
$(x-y)^2=13-3y^2=13$ (loại vì 13 không là scp)
Với $y^2=1$:
$(x-y)^2=13-3y^2=10$ (loại vì 10 không là scp)
Với $y^2=4$:
$(x-y)^2=13-3y^2=1$
$\Rightarrow x-y=\pm 1$
$\Rightarrow x=y\pm 1$
$y^2=4\Rightarrow y=\pm 2$
Với $y=2$ thì $x=1$ hoặc $x=3$
Với $y=-2$ thì $x=-3$ hoặc $y=-1$
Đúng 1
Bình luận (0)
Tìm nghiệm nguyên dương của phương trình : 2xy - 6x - 5y =3041994
Tìm giá trị nhỏ nhất của số nguyên dương k sao cho phương trình 2xy - 3x - 5y = k có một số lẻ các nghiệm nguyên dương
Tìm nghiệm nguyên dương của phương trình:
xy2+2xy+243y+x=0
VT >0 với mọi x,y dương nên phương trình vô nghiệm
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên dương của phương trình:
xy2+2xy-243y+x=0