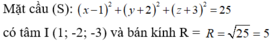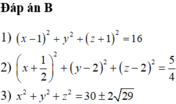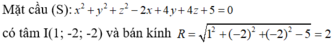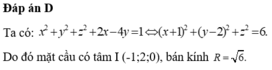Tìm tâm và bán kính của mặt cầu có phương trình: x2 + (y + 5)2 + (z + 1)2 = 2

Những câu hỏi liên quan
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 25
Tìm tọa độ tâm I và bán kính R của mặt cầu (S)
A. I(1; -2; -3); R = 25
B. I(-1; 2; 3); R = 5
C. I(-1; 2; 3); R = 25
D. I(1; -2; -3); R = 5
Trong không gian Oxyz, cho mặt cầu (S)có phương trình
(
x
-
1
)
2
+
(
y
-
2
)
2
+
(
z
-
3
)
2
25
. Tọa độ tâm I và bán kính R của (S) là A. I(1;2;3) và R5. B. I(-1;-2;-3) và R5. C. I(1;2;3) và R25. D. I(-1;-2;-3) và R25
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S)có phương trình ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 . Tọa độ tâm I và bán kính R của (S) là
A. I(1;2;3) và R=5.
B. I(-1;-2;-3) và R=5.
C. I(1;2;3) và R=25.
D. I(-1;-2;-3) và R=25
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²+2x-4y+6z-20. Tìm tọa độ tâm I và tính bán kính R của (S). A. Tâm I(-1;2;-3) và bán kính R4 B. Tâm I(1;-2;3) và bán kính R4 C. Tâm I(-1;2;3) và bán kính R4 D. Tâm I(1;-2;3) và bán kính R16.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²+2x-4y+6z-2=0. Tìm tọa độ tâm I và tính bán kính R của (S).
A. Tâm I(-1;2;-3) và bán kính R=4
B. Tâm I(1;-2;3) và bán kính R=4
C. Tâm I(-1;2;3) và bán kính R=4
D. Tâm I(1;-2;3) và bán kính R=16.
Đáp án A
Ta có (S): (x+1)²+(y-2)²+(z+3)²=16.
Do đó mặt cầu (S) có tâm I(-1;2;-3) và bán kính R=4.
Đúng 0
Bình luận (0)
Cho mệnh đề:1) Mặt cầu có tâm I(1;0;-1), đường kính bằng 8 là:
(
x
-
1
)
2
+
y
2
+
(
z
+
1
)
2
16
2) Mặt cầu có đường kính AB với A(-1;2;1),B(0;2;3) là:
(
x
+
1
2
)
2...
Đọc tiếp
Cho mệnh đề:
1) Mặt cầu có tâm I(1;0;-1), đường kính bằng 8 là: ( x - 1 ) 2 + y 2 + ( z + 1 ) 2 = 16
2) Mặt cầu có đường kính AB với A=(-1;2;1),B=(0;2;3) là: ( x + 1 2 ) 2 + ( y - 2 ) 2 + ( z - 2 ) 2 = 5 4
3) Mặt cầu có tâm O(0;0;0) và tiếp xúc với mặt cầu (S) có tâm (3;-2;4), bán kính bằng 1 là: x 2 + y 2 + z 2 = 30 ± 2 29
Số mệnh đề đúng là bao nhiêu:
A. 2
B. 1
C. 3
D. 0
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình (x+1)²+(y-3)²+z²16. Tìm tọa độ tâm I và bán kính R của mặt cầu đó. A. I(-1;3;0), R4 B. I(1;-3;0), R4 C. I(-1;3;0), R16 D. I(1;-3;0), R16.
Đọc tiếp
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình (x+1)²+(y-3)²+z²=16. Tìm tọa độ tâm I và bán kính R của mặt cầu đó.
A. I(-1;3;0), R=4
B. I(1;-3;0), R=4
C. I(-1;3;0), R=16
D. I(1;-3;0), R=16.
Đáp án A
Tọa độ tâm và bán kính của mặt cầu là I(-1;3;0), R=4.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
x
2
+
y
2
+
z
2
- 2x + 4y + 4z + 5 0Tìm tọa độ tâm I và bán kính R của mặt cầu (S) A. I(1; -2; -2); R 2 B. I(1; -2; -2); R 4 C. I(-1; 2; 2); R 2 D. I(-2; 4; 4); R 4
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
x 2 + y 2 + z 2 - 2x + 4y + 4z + 5 = 0
Tìm tọa độ tâm I và bán kính R của mặt cầu (S)
A. I(1; -2; -2); R = 2
B. I(1; -2; -2); R = 4
C. I(-1; 2; 2); R = 2
D. I(-2; 4; 4); R = 4
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²-2x+4y-6z+90. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S). A. I(-1;2;3), R√5 B. I(1;-2;3), R√5 C. I(1;-2;3), R5 D. I(-1;2;-3), R5.
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²-2x+4y-6z+9=0. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S).
A. I(-1;2;3), R=√5
B. I(1;-2;3), R=√5
C. I(1;-2;3), R=5
D. I(-1;2;-3), R=5.
Trong không gian với trục tạo độ Oxyz, cho
x
2
+
y
2
+
z
2
+
2
x
−
4
y
+
6
z
−
2
0
là phương trình mặt cầu (S). Mặt cầu (S) đồng tâm với mặt cầu (S) (có tâm trùng với tâm mặt cầu (S)) và đi qua điểm M(1;3;-1). Khi đó, bán kính R của mặt cầu (S) bằng bao nhiêu? A. ...
Đọc tiếp
Trong không gian với trục tạo độ Oxyz, cho x 2 + y 2 + z 2 + 2 x − 4 y + 6 z − 2 = 0 là phương trình mặt cầu (S). Mặt cầu (S') đồng tâm với mặt cầu (S) (có tâm trùng với tâm mặt cầu (S)) và đi qua điểm M(1;3;-1). Khi đó, bán kính R của mặt cầu (S') bằng bao nhiêu?
A. R = 3 .
B. R = 41 .
C. R = 4.
D. R = 3.
Trong không gian với trục tọa độ Oxyz, cho
x
2
+
y
2
+
z
2
+2x-4y+6z-20 là phương trình mặt cầu (S). Mặt cầu
(
S
)
đồng tâm với mặt cầu (S) (có tâm trùng với tâm mặt cầu (S)) và đi qua điểm M (1;3;-1). Khi đó, bán kính R của mặt cầu
(
S
)
bằng...
Đọc tiếp
Trong không gian với trục tọa độ Oxyz, cho x 2 + y 2 + z 2 +2x-4y+6z-2=0
là phương trình mặt cầu (S). Mặt cầu ( S ' ) đồng tâm với mặt cầu (S)
(có tâm trùng với tâm mặt cầu (S)) và đi qua điểm M (1;3;-1). Khi đó,
bán kính R của mặt cầu ( S ' ) bằng bao nhiêu
![]()
![]()
![]()
![]()
Tìm tọa độ tâm I bán kính R của mặt cầu có phương trình x 2 + y 2 + z 2 + 2 x - 4 y = 1
A. I(1;-2;0), R=1
B. I(-1;2;0), R=1
C. I(1;-2;0), R= 6
D. I(-1;2;0), R= 6