\(D=\frac{sin4x+sin5x+sin6x}{cos4x+cos5x+cos6x}\)

\(=\frac{\left(sin4x+sin6x\right)+sin5x}{\left(cos4x+cos6x\right)+cos5x}\)

\(=\frac{2sin\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+sin5x}{2cos\frac{4x+6x}{2}.cos\frac{4x-6x}{2}+cos5x}\)

\(=\frac{2sin5x.cos\left(-x\right)+sin5x}{2cos5x.cos\left(-x\right)+cos5x}=\frac{sin5x\left(2.cos\left(-x\right)+1\right)}{cos5x\left(2.cos\left(-x\right)+1\right)}=\frac{sin5x}{cos5x}=tan5x\)

\(D=\frac{1+sin2x+cos2x}{1+sin2x-cos2x}=\frac{1+2sinxcosx+2cos^2x-1}{1+2sinxcosx-1+2sin^2x}\)

\(D=\frac{cosx\left(sinx+cosx\right)}{sinx\left(sinx+cosx\right)}=cotx\)

\(F=\frac{sinx+sin4x+sin7x}{cosx+cos4x+cos7x}\)

\(F=\frac{2sin4xcos3x+sin4x}{2cos4xcos3x+cos4x}\)

\(F=\frac{2sin4x\left(cos3x+1\right)}{2cos4x\left(cos3x+1\right)}=tan4x\)

\(G=\frac{cos2x-sin4x-cos6x}{cos2x+sin4x-cos6x}=\frac{-2sin4xsin2x-sin4x}{-2sin4xsin2x+sin4x}\)

\(G=\frac{-sin4x\left(2sin2x+1\right)}{-sin4x\left(2sin2x-1\right)}=\frac{2sin2x+1}{2sin2x-1}\)

Chọn A

y = cos6 x+ sin2xcos2x(sin2x + cos2x) + sin4x - sin2x

= cos6x + sin2x(1 - sin2x) + sin4x - sin2x = cos6x

Do đó : y' = -6cos5xsinx.

Ta có:

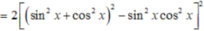
Vậy giá trị của biểu thức  không phụ thuộc vào x.

\( 2)\sin x + \sin 2x + \sin 3x = 0\\ \Leftrightarrow 2\sin 2x.\cos x + \sin 2x = 0\\ \Leftrightarrow \sin 2x\left( {2\cos x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin 2x = 0\\ 2\cos x + 1 = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} 2x = k\pi \\ \cos x = \dfrac{{ - 1}}{2} \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{k\pi }}{2}\\ x = \pm \dfrac{{2\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z} } \right) \)

\( 3)\sin x + \sin 2x + \sin 3x + \sin 4x = 0\\ \Leftrightarrow \left( {\sin x + \sin 4x} \right) + \left( {\sin 2x + \sin 3x} \right) = 0\\ \Leftrightarrow 2\sin \dfrac{{5x}}{2}.\cos \dfrac{{3x}}{2} + 2\sin \dfrac{{5x}}{2}.\cos \dfrac{x}{2} = 0\\ \Leftrightarrow \sin \dfrac{{5x}}{2}.\left( {\cos \dfrac{{3x}}{2} + \cos \dfrac{x}{2}} \right) = 0\\ \Leftrightarrow \sin \dfrac{{5x}}{2}.2\cos x.\cos \dfrac{x}{2} = 0\\ \Leftrightarrow \left[ \begin{array}{l} \sin \dfrac{{5x}}{2} = 0\\ 2\cos x = 0\\ \cos \dfrac{x}{2} = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = \dfrac{{2k\pi }}{5}\\ x = \dfrac{\pi }{2} + k\pi \\ x = \pi + 2k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \)