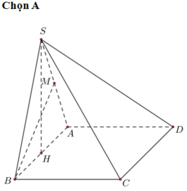
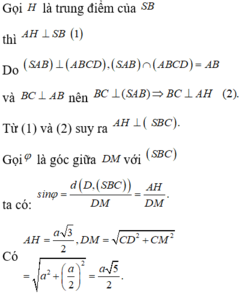Các bạn cho mình hỏi lúc nào đường cao của hình chọp cũng vuông góc vơi s mặt phẳng đáy của hai đường chéo đa giác đều ạ

Những câu hỏi liên quan
Trong các phát biểu sau, phát biểu nào đúng?a) Hình chóp đều S.ABCD có đáy là hình bình hành.b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
Đọc tiếp
Trong các phát biểu sau, phát biểu nào đúng?
a) Hình chóp đều S.ABCD có đáy là hình bình hành.
b) Hình chóp đều S.ABCD có đáy là hình thoi, chân đường cao hình chóp là giao điểm của 2 đường chéo hình thoi.
c) Hình chóp đều S.ABCD có đáy là hình vuông, chân đường cao hình chóp là giao điểm của 2 đường chéo hình vuông.
d) Hình chóp đều S.ABCD có đáy là hình vuông, các mặt bên là các tam giác đều chung đỉnh S.
: Nếu đặt mặt đáy của hình chóp đều đáy là hình vuông song song với mặt phẳng chiếu bằng thì hình chiếu bằng là hình
A. chữ nhật có hai đường chéo. B. vuông có hai đường chéo. C.tròn. D.tam giác đều.
1,Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy, SAa√6,ABa. a/Chứng minh các mặt bên của hình chóp là các tam giác vuôngb/ Xác định và tính góc giữa đường thẳng SC và mặt đáy (ABC) 2,Cho hình chóp S. MNPQ là hình vuông cạnh a SM vuông góc với mặt phẳng (MNPQ),SMa√2.a/ Chứng minh QN vuông góc với mặt phẳng (SMP).b/ Trong tam giác SMQ dựng đường cao MH, chứng minh MH vuông góc với SP. c/ Xác định và tính khoảng cách giữa hai đường thẳng MN và SQGIÚP MÌNH VỚI Ạ...
Đọc tiếp
1,Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy, SA=a√6,AB=a.
a/Chứng minh các mặt bên của hình chóp là các tam giác vuông
b/ Xác định và tính góc giữa đường thẳng SC và mặt đáy (ABC)
2,Cho hình chóp S. MNPQ là hình vuông cạnh a SM vuông góc với mặt phẳng (MNPQ),SM=a√2.
a/ Chứng minh QN vuông góc với mặt phẳng (SMP).
b/ Trong tam giác SMQ dựng đường cao MH, chứng minh MH vuông góc với SP.
c/ Xác định và tính khoảng cách giữa hai đường thẳng MN và SQ
GIÚP MÌNH VỚI Ạ
MÌNH CẢM ƠN 💙💙💙
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD. Hỏi góc giữa hai đường thẳng TB và BD nằm trong khoảng nào dưới đây
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD. Hỏi góc giữa hai đường thẳng TB và BD nằm trong khoảng nào dưới đây


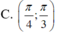
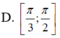
Chọn đáp án A
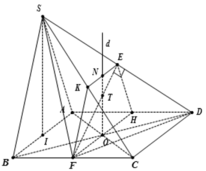
+ Gọi O là tâm của hình vuông ABCD. Qua O ta dựng đường thẳng d vuông góc với mặt đáy.
+ Gọi E, K, F, H, N lần lượt là trung điểm của các đoạn thẳng SD, SC, BC, AD, EK
+ Ta có tam giác SDF là tam giác cân tại F. Vì FD = FS = a 5 (độc giả tự chứng minh)
Suy ra FE ⊥ SD
Mặt khác, ta có KE // FH (Vì cùng song song với CD). Nên 4 điểm K, E, F, H đồng phẳng
+ Trong mặt phẳng (KEFH), gọi T là giao điểm của FE và ON.
Ta có T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD
+ Ta có tam giác EKO là tam giác đều cạnh a. Nên
![]()
Bán kính mặt cầu là
![]()
+ Xét tam giác vuông TOB vuông tại B, ta có
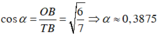
Đúng 0
Bình luận (0)
Cho hình lăng trụ tam giác đều
A
B
C
.
A
1
B
1
C
1
có cạnh đáy bằng 2, độ dài đường chéo của các mặt bên bằng
5
. Số đo góc giữa hai mặt phẳng
(
A
1
B
C
)
và
(
A
B
C
)
là A. ...
Đọc tiếp
Cho hình lăng trụ tam giác đều A B C . A 1 B 1 C 1 có cạnh đáy bằng 2, độ dài đường chéo của các mặt bên bằng 5 . Số đo góc giữa hai mặt phẳng ( A 1 B C ) và ( A B C ) là
A. 45 o
B. 90 o
C. 60 o
D. 30 o
Cho hình lăng trụ tam giác đều
A
B
C
.
A
1
B
1
C
1
có cạnh đáy bằng 2, độ dài đường chéo của các mặt bên bằng
5
. Số đo góc giữa hai mặt phẳng
(
A
1
B
C
)
và
(
A
B
C
)
là A. ...
Đọc tiếp
Cho hình lăng trụ tam giác đều A B C . A 1 B 1 C 1 có cạnh đáy bằng 2, độ dài đường chéo của các mặt bên bằng 5 . Số đo góc giữa hai mặt phẳng ( A 1 B C ) và ( A B C ) là
A. 45 0 .
B. 90 0 .
C. 60 0 .
D. 30 0 .
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC. A.
a
3
2
B. a C.
a
3
4
D.
a
2
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC.
A. a 3 2
B. a
C. a 3 4
D. a 2
Nếu đặt mặt đáy của hình chóp đều có đáy hình vuông song song với mặt phẳng chiếu cạnh thì hình chiếu cạnh của nó là:
Hình tam giác cân
Hình tam giác đều
Hình vuông
Hình vuông có hai đường chéo
Cho hình chóp S. ABCD có đáy là hình vuông cạnh a tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính sinh của góc tạo bởi đường thẳng MD và mặt phẳng (SBC) với M là trung điểm của BC A.
15
5
B.
15
3
C.
13
3
D.
13
5
Đọc tiếp
Cho hình chóp S. ABCD có đáy là hình vuông cạnh a tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính sinh của góc tạo bởi đường thẳng MD và mặt phẳng (SBC) với M là trung điểm của BC
A. 15 5
B. 15 3
C. 13 3
D. 13 5