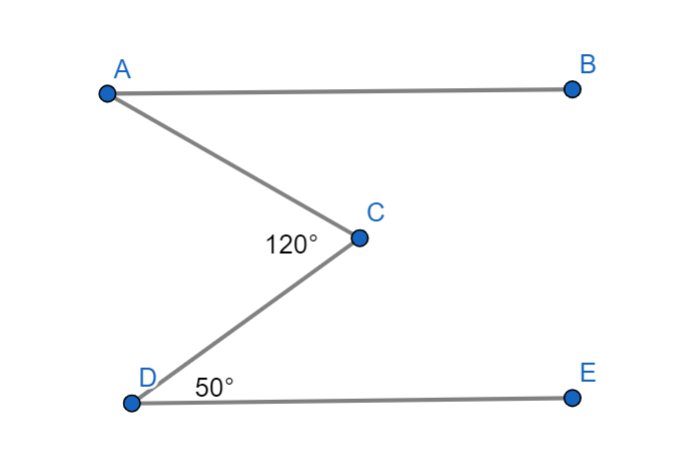
 Cho AB//DE. Tính CAB
Cho AB//DE. Tính CAB

Những câu hỏi liên quan
Cho tam giác ABC Có Góc A = 90 , AB=3,AC=4 , tia phân giác góc A cắt Bc tại D . Từ D kẻ DE vuông góc với AC tại E. A)DB/DC = ? DB=? DC=? (BD/DC=3/4 DB=6,4 DC=8,6) B) Tam giác CED Đông dang vs tam giác CAB (Ko cần làm) C) Tính DE = ? ( DE=5,16)Sadb/Sadc
Cho hai tam giác ABC và DEF .có BC = EF ; AB = DE ; AC = DF . Ta có:
A. ∆ ABC = ∆ DEF B. ∆ ABC = ∆ EDF
C. ∆ CAB = ∆ DFE D. ∆ BAC = ∆ DFE
Cho hai tam giác ABC và DEF .có BC = EF ; AB = DE ; AC = DF . Ta có:
A. ∆ ABC = ∆ DEF B. ∆ ABC = ∆ EDF
C. ∆ CAB = ∆ DFE D. ∆ BAC = ∆ DFE
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A , đg cao AH a) cm tam giác AHB đồng dạng với tam giác CAB . Và AH.CB=AB.AC b) Gọi D, E lần lượt là hình chiếu của H trên Ab , AC .Tứ giác DEHA là hình gì?Vì sao??? c) Cho AB=9cm , AC=12cm . tính DE d) cm : AH^2 = DA.DB+EA.EC
a: Xét ΔAHB vuông tạiH và ΔCAB vuông tại A có
góc B chung
=>ΔAHB đồng dạng với ΔCAB
b: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
c:
\(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
\(AH=\dfrac{9\cdot12}{15}=7.2\left(cm\right)\)
=>DE=7,2cm
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AD . trên tia đối của tia CB lấy điểm E sao cho AC là tia phân giác của góc DAE.
a\ cmr : tam giác ADB đồng dạng với tam giác CAB
b\ bt AB=12 cm, AC=9cm . tính AD
c\ cmr : CDtrên CE=BD trên DE
Cho đường tròn (O; 2cm), AB là đường kính, vẽ dây AC sao cho góc CAB bằng 50°. Tính BC
Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
Xét ΔCAB vuông tại C có \(sinCAB=\dfrac{CB}{AB}\)
=>\(CB=AB\cdot sinCAB=4\cdot sin50\simeq3,06\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC, vẽ tia phân giác AD của góc BAC ( D € BC). Tại D vẽ DE//AB ( E€ AC )
a) Chứng minh EAD = EDA
b) Vẽ EF // AD ( F € BC ). Chứng minh CEF = CAB : 2
Cho 2 tam giác ABC và ADE không có điểm trong chung,có 2 cặp cạnh bằng nhau : AB = AD , AC = AE và cặp góc xen giữa bù nhau CAB + DAE = 180 độ .Gọi M là trung điểm của BC ,cm : AM = 1/2 DE
Cho tam giác ABC cân tại A . M là trung điểm AB . Góc CAB= 20 độ . Tính góc CMB
Cho tam giác ABC vuông tại A, AB = 9cm, BC = 15cm, đường cao AH a) Chứng minh tam giác AHB ~tam giác CAB, tam giác CHA tam giác CAB b) Chứng minh AH = BH. CH. Tính BH, CH, NH c) Tính tỉ số diện tích tam giác CHA và tam giác AHE
a: Xet ΔAHB vuông tại H và ΔCAB vuông tại A có
góc B chung
=>ΔAHB đồng dạng với ΔCAB
Xét ΔCHA vuông tại H và ΔCAB vuông tại A có
góc C chung
=>ΔCHA đồng dạng với ΔCAB
b: Xét ΔABC vuông tại A có AH là đường cao
nênAH^2=HB*HC
Đúng 1
Bình luận (0)
Trên tia Ox xác định điểm A và B sao cho OA = 3cm, OB = 7cm
a) Tinh độ dài đoạn AB
b) Vẽ tia AC sao cho góc CAB = 60 độ. Tính góc CAO
c) Vẽ tia Am và An lần lượt là phân giác của góc CAO và góc CAB. Tính góc mAn


















