cho a,b,c là ba cạnh tam giác. c/m: abc >hoặc = (b+c-a)*(a+c-b)*(a+b-c)

Những câu hỏi liên quan
cho tam giác ABC với a; b ; c là độ dài ba cạnh tam giác. Chứng minh:
a^2(b+c-a)+b^2(c+a-b)+c^2(a+b-c)<=3abc
cho a,b,c là 3 cạnh tam giác.c/m: abc > hoặc = ( a + b - c ).( b + c - a ).( c + a - b)
cho a,b,c là ba cạnh của tam giác c/m:
A= a/(b+c-a) + b/(a+c-b) +c/(a+b-c) lớn hơn hoặc bằng 3
cần gấp ai làm hộ thành thật rất cảm ơn
làm hơn tắt cũng được
cau h cho minh di nhe
cua minh co chu chip chip day
Đúng 0
Bình luận (0)
cho tam giác ABC có độ dài ba cạnh lần lượt là a, b , c . Biết 2p = a + b +
chứng minh rằng 1/p-a + 1/p-b + 1/p-c > hoặc bằng 2 ( 1/a + 1/b + 1/c )
dấu bằng trong bất đẳng thức trên xảy ra khi tam giác ABC có đặc điểm gì
C/m BĐT phụ: \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\) (*) (x,y dương)
Ta có: \(\left(x-y\right)^2\ge0\)
\(\Leftrightarrow\)\(x^2-2xy+y^2\ge0\)
\(\Leftrightarrow\)\(x^2+y^2\ge2xy\)
\(\Leftrightarrow\)\(x^2+2xy+y^2\ge4xy\)
\(\Leftrightarrow\)\(\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow\)\(\frac{x+y}{xy}\ge\frac{4}{x+y}\)
\(\Leftrightarrow\)\(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\) (BĐT đã đc chứng minh)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y\)
ÁP dụng BĐT (*) ta có:
\(\frac{1}{p-a}+\frac{1}{p-b}\ge\frac{4}{p-a+p-b}=\frac{4}{2p-\left(a+b\right)}=\frac{4}{c}\) (1)
\(\frac{1}{p-b}+\frac{1}{p-c}\ge\frac{4}{p-b+p-c}=\frac{4}{2p-\left(b+c\right)}=\frac{4}{a}\) (2)
\(\frac{1}{p-c}+\frac{1}{p-a}\ge\frac{4}{p-c+p-a}=\frac{4}{2p-\left(c+a\right)}=\frac{4}{b}\) (3)
Lấy (1); (2); (3) cộng theo vế ta được:
\(2\left(\frac{1}{p-a}+\frac{1}{p-b}+\frac{1}{p-c}\right)\ge4\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
\(\Leftrightarrow\)\(\frac{1}{p-a}+\frac{1}{p-b}+\frac{1}{p-c}\ge2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\) (đpcm)
Dấu "=" xảy ra \(\Leftrightarrow\)\(a=b=c\)
Khi đó \(\Delta ABC\)là tam giác đều
Đúng 0
Bình luận (0)
Cho a, b ,c là độ dài 3 cạnh của 1 tam giác.
Chứng minh rằng: abc lớn hơn hoặc bằng (a+b-c)(a+c-b)(b+c-a)
vì a;b;c là độ dài 3 cạnh của 1 tam giác áp dụng bđt tam giác ta có\(\Rightarrow\hept{\begin{cases}a+b>c\Rightarrow a+b-c>0\\a+c>b\Rightarrow a+c-b>0\\b+c>a\Rightarrow b+c-a>0\end{cases}}\)
\(\Rightarrow\sqrt{a+b-c};\sqrt{a+c-b};\sqrt{b+c-a}\)luôn được xác định\(\left(\sqrt{a+b-c}-\sqrt{a+c-b}\right)>=0\Rightarrow a+b-c-2\sqrt{\left(a+b-c\right)\left(a+c-b\right)}+a+c-b\)\(>=0\Rightarrow a+b-c+a+c-b>=2\sqrt{\left(a+b-c\right)\left(a+c-b\right)}\Rightarrow\frac{a+b-c+a+c-b}{2}=\frac{2a}{2}\)
\(=a>=\sqrt{\left(a+b-c\right)\left(a+c-b\right)}\)
tương tự ta có :\(b>=\sqrt{\left(a+b-c\right)\left(b+c-a\right)};c>=\sqrt{\left(a+c-b\right)\left(b+c-a\right)}\)
\(\Rightarrow abc>=\sqrt{\left(a+b-c\right)^2\left(a+c-b\right)^2\left(b+c-a\right)^2}=\left(a+b-c\right)\left(a+c-b\right)\left(b+c-a\right)\)
dấu = xảy ra khi a=b=c
Đúng 0
Bình luận (0)
dòng 3 là vì \(\left(\sqrt{a+b-c}-\sqrt{a+c-b}\right)^2>=0\)nhá
Đúng 0
Bình luận (0)
Cho a ; b; c là ba cạnh của một tam giác vuông trong đó c là cạnh huyền.
Tìm \(A=\dfrac{a^2\left(b+c\right)+b^2\left(a+c\right)}{abc}\)
Tìm điều gì của A em? Chứ với mỗi một bộ số a;b;c sẽ cho 1 kết quả A khác nhau rồi đó
Đúng 0
Bình luận (0)
\(A=\dfrac{a^2b}{abc}+\dfrac{a^2c}{abc}+\dfrac{ab^2}{abc}+\dfrac{b^2c}{abc}=\dfrac{a}{c}+\dfrac{a}{b}+\dfrac{b}{a}+\dfrac{b}{c}=\dfrac{a^2+b^2}{ab}+\dfrac{a+b}{c}\)
\(A=\dfrac{c^2}{ab}+\dfrac{a+b}{c}\ge\dfrac{4c^2}{\left(a+b\right)^2}+\dfrac{a+b}{c}\)
\(A\ge\dfrac{a+b}{2c}+\dfrac{a+b}{2c}+\dfrac{\sqrt{2}c^2}{\left(a+b\right)^2}+\dfrac{\left(4-\sqrt{2}\right)c^2}{\left(a+b\right)^2}\)
\(A\ge3\sqrt[3]{\dfrac{\left(a+b\right)^2\sqrt{2}c^2}{4c^2\left(a+b\right)^2}}+\dfrac{\left(4-\sqrt{2}\right)c^2}{2\left(a^2+b^2\right)}=2+\sqrt{2}\)
Dấu "=" xảy ra khi \(a=b=\dfrac{c}{\sqrt{2}}\)
Đúng 1
Bình luận (0)
Cho a,b,c là độ dài 3 cạnh của một tam giác
Chứng minh :(a+b-c)(b+c-a)(c+a-b) <=(bé hơn hoặc bằng) abc
Vì a:b:c là độ dài cạnh tam giác nên \(\hept{\begin{cases}a+b>c\\b+c>a\\c+a>b\end{cases}\Rightarrow\hept{\begin{cases}a+b-c>0\\b+c-a>0\\c+a-b>0\end{cases}}}\)
Áp dụng bđt AM - GM ta có :
\(\sqrt{\left(a+b-c\right)\left(b+c-a\right)}\le\frac{a+b-c+b+c-a}{2}=\frac{2b}{2}=b\)(1)
\(\sqrt{\left(a+b-c\right)\left(c+a-b\right)}\le\frac{a+b-c+c+a-b}{2}=\frac{2a}{2}=a\)(2)
\(\sqrt{\left(b+c-a\right)\left(c+a-b\right)}\le\frac{b+c-a+c+a-b}{2}=\frac{2c}{2}=c\)(3)
Nhân vế với vế của (1); (2);(3) lại ta được :
\(\sqrt{\left(a+b-c\right)^2\left(b+c-a\right)^2\left(c+a-b\right)^2}\le abc\)
\(\Leftrightarrow\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\le abc\)(đpcm)
Đúng 0
Bình luận (0)
Cho ba cạnh của tam giác ABC là a,b,c Chứng minh tam giác ABC đều với các đẳng thức sau
a)(a+b+c)^2=3(ab+bc+ca)
b)a^3+b^3+c^3-3abc=0
c)(a+b)(b+c)(c+a)=8abc
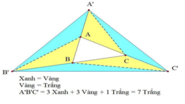
Cho tam giác ABC. Kéo dài cạnh BC về phía B một đoạn BB/ bằng CB, kéo dài cạnh BA về phía A một đoạn AA/ bằng BA, kéo dài cạnh AC về phía C một đoạn CC/ bằng AC. Nối A/B/; B/C/; C/A/. Diện tích tam giác A/B/C/ so với diện tích tam giác ABC thì gấp?