Cho nửa đường tròn tâm O có đường kính AB, C là một điểm thuộc nửa đường tròn. Qua C kẻ tiếp tuyến d với nửa đường tròn. Kẻ các tia Ax, By song song với nhau, cắt d theo thứ tự tại D, E. Chứng minh rằng AB là tiếp tuyến của đường tròn đường kính DE.

Những câu hỏi liên quan
Cho nửa đường tròn tâm O có đường kính AB, C là một điểm thuộc nửa đường tròn. Qua C kẻ tiếp tuyến d với nửa đường tròn. Kẻ các tia Ax, By song song với nhau, cắt d theo thứ tự tại D, E. Chứng minh rằng AB là tiếp tuyến của đường tròn đường kính DE.
mong mọi giúp với ạ thank
Cho nửa đường tròn tam o đường kính ab, c là 1 điểm thuộc nửa đường tròn. Qua c kẻ tiếp tuyến d vs nửa đường tròn. Kẻ tia ax, by song song vs nhau, cắt d theo thứ tự tại D, E. Chứng minh ab là tiếp tuyến của đường tròn đường kính DE
Cho nửa đường tròn tâm O có đường kính AB 2R. Kẻ hai tiếp tuyến Ax. By của nửa đường tròn (O) tại A, B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn cắt tia Ax và By theo thứ tự tại C và D.A) chứng minh AC. BDR2B) kẻ MH vuông góc AB(H thuộc AB) chứng minh :OC song song với BM. C) chứng minh rằng BC đi qua trung điểm đoạn MH
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax. By của nửa đường tròn (O) tại A, B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn cắt tia Ax và By theo thứ tự tại C và D.
A) chứng minh AC. BD=R2
B) kẻ MH vuông góc AB(H thuộc AB) chứng minh :OC song song với BM.
C) chứng minh rằng BC đi qua trung điểm đoạn MH
Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng: ∠COD 90o
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:
∠COD = 90o
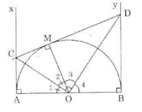
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OC là tia phân giác của ∠AOM
OD và tia phân giác của ∠BOM
OC và OD là các tia phân giác của hai góc kề bù ∠AOM và ∠BOM nên OC ⊥ OD.
=> ∠COD = 90o (đpcm)
Đúng 2
Bình luận (0)
Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng: CD AC + BD
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:
CD = AC + BD
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = AC, DM = BC
Do đó: CD = CM + DM = AC + BD (đpcm)
Đúng 0
Bình luận (0)
cho nửa đường tròn tâm O đường kính AB2R .kẻ các tuyến tiếp Ax,By với nửa đường tròn (Ax ,By năm cùng phía với nửa đường tròn O) gọi M là một điểm trên nửa đường tròn (M khác A và B) tiếp tuyến kẻ từ M của nửa đường tròn O cắt Ax ,By thứ tự ở C và D chứng minh a) bốn điểm O,M,D,B thẳng hàng b) COvuông góc OD c) gọi I là giao điểm của AD và BC chứng minh MI song song BD thầy ơi giúp e với
Đọc tiếp
cho nửa đường tròn tâm O đường kính AB=2R .kẻ các tuyến tiếp Ax,By với nửa đường tròn (Ax ,By năm cùng phía với nửa đường tròn O) gọi M là một điểm trên nửa đường tròn (M khác A và B) tiếp tuyến kẻ từ M của nửa đường tròn O cắt Ax ,By thứ tự ở C và D chứng minh a) bốn điểm O,M,D,B thẳng hàng b) COvuông góc OD c) gọi I là giao điểm của AD và BC chứng minh MI song song BD thầy ơi giúp e với
Cho nửa đường tròn tâm (O) có đường kính AB 2R. Kẻ hai tiếp tuyến Ax , By của nửa đường tròn (O) tại A và B (Ax , By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn(M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D 1) Chứng minh tam giác COD vuông tại O 2) Chứng minh AC.BD R2 3)Kẻ MH vuông góc AB (H thuộc AB). Chứng minh rằng BC đi qua trung điểm của đoạn MHgiúp mik với
Đọc tiếp
Cho nửa đường tròn tâm (O) có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax , By của nửa đường tròn (O) tại A và B (Ax , By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn(M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D
1) Chứng minh tam giác COD vuông tại O
2) Chứng minh AC.BD = R2
3)Kẻ MH vuông góc AB (H thuộc AB). Chứng minh rằng BC đi qua trung điểm của đoạn MH
giúp mik với
Cho nửa đường tròn tâm O đường kính AB. Vẽ các tiếp tuyến Ax, By của nửa đường tròn. Kẻ tiếp tuyến tại M là 1 điểm bất kỳ thuộc đường tròn. Tiếp tuyến này cắt Ax, By thứ tự tại C, D. Chứng minh đường tròn đường kính CD tiếp xúc với AB
Câu 3(3đ) Cho nửa đường tròn tâm O,đường kính AB. Vẽ các tiếp tuyến Ax , By cùng phía với nửa đường tròn đối với AB. Qua điểm E thuộc nửa đường tròn (E khác A và B) kẽ tiếp tuyến với nửa đường tròn, nó cắt Ax , By theo thứ tự ở C và Da)Chứng minh rằng : CD AC + BD b)Tính số đo góc ? c)Tính : AC.BD ( Biết OA 6cm)
Đọc tiếp
Câu 3(3đ) Cho nửa đường tròn tâm O,đường kính AB. Vẽ các tiếp tuyến Ax , By cùng phía với nửa đường tròn đối với AB. Qua điểm E thuộc nửa đường tròn (E khác A và B) kẽ tiếp tuyến với nửa đường tròn, nó cắt Ax , By theo thứ tự ở C và D
a)Chứng minh rằng : CD = AC + BD b)Tính số đo góc ? c)Tính : AC.BD ( Biết OA = 6cm)
a: Xét (O) có
CE,CA là các tiếp tuyến
nên CE=CA và OC là phân giác của góc AOE(1)
Xét (O) có
DE,DB là các tiếp tuyến
nên DE=DB vàOD là phân giác của góc BOE(2)
CD=CE+ED
=>CD=CA+BD
b: Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CE*ED=OE^2=R^2=36cm
Đúng 3
Bình luận (0)













