Cho Ax và By là 2 tiếp tuyến song song của đường tròn O. (A,B thuộc (O) )
a) Chứng minh AB là đường kính của ( O)
b) 1 tiết tuyến thứ 3 của đường tròn O cắt Ax và By. Làn lượt tại M và N. Biết AM=3.2 cm , BN= 5 cm .Tình bán kính của đường tròn O
Những câu hỏi liên quan
Cho Ax, By là 2 tiếp tuyến song song của đường tròn (O) (A,B là các tiếp điểm)
a) Chứng minh rằng : AB là đường kính của đường tròn
b) 1 tiếp tuyến thứ 3 của (O) cắt Ax, By lần lượt tại M và N. Biết AM=3,2; BN=5. Tính bán kính của (O)
trên google có đầy rùi đăng lạm gì nữa
Đúng 0
Bình luận (0)
Cho Ax,By là 2 tiếp tuyến song song của đường tròn (O) (A,B là các tiếp điểm)
a) Chứng minh rằng AB là đường kính của đường tròn
b) Cho 1 tiếp tuyến thứ 3 của (O) cắt Ax,By lần lượt tại M và N. Biết AM=3, BN =5. Tính bán kính của đường tròn
Giải dùm mk đi mk cần gấp lm
1) Cho Ax, By là các tiếp tuyến song song của đường tròn tâm O. (A,B là các tiếp điểm)
a, Chứng minh: AB là đường kính đường tròn O
b) Một tiếp tuyến thứ 3 của đường tròn O cắt Ax, By ở M,N. Biết AM=3,2 và BN=5. Tính bán kính của hình tròn
Số cây cam là:
120 : ( 2 + 3 ) x 2 = 48 (cây)
Số cây xoài là:
( 1 + 5 ) = 20 ( cây )
Số cây chanh là:
120 - ( 48 + 20 ) = 52 ( cây )
Đáp số : cam : 48 cây
xoài : 20 cây
chanh : 52 cây.
ai trên 10 điểm thì mình nha
Đúng 0
Bình luận (0)
Cho Ax, By là các tiếp tuyến song song của đường tròn tâm O. (A,B là các tiếp điểm)
a, Chứng minh: AB là đường kính đường tròn O
b) Một tiếp tuyến thứ 3 của đường tròn O cắt Ax, By ở M,N. Biết AM=3,2 và BN=5. Tính bán kính của hình tròn.
Số cây cam là:
120 : ( 2 + 3 ) x 2 = 48 (cây)
Số cây xoài là:
( 1 + 5 ) = 20 ( cây )
Số cây chanh là:
120 - ( 48 + 20 ) = 52 ( cây )
Đáp số : cam : 48 cây
xoài : 20 cây
chanh : 52 cây.
ai trên 10 điểm thì mình nha
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O có đường kính AB . Gọi Ax , By là hai tiếp tuyến vẽ từ A đến B ( Ax , By và nửa đường tròn cùng thuộc nửa mặt phẳng bờ AB) . Qua điểm thuộc nửa đường tròn ( M khác A và B ) kẻ tiếp tuyến thứ ba , tiếp tuyến này cắt Ax và By lần lượt tại điểm C và D 1. Chứng minh CD=AC+BD.
2. Gọi N là giao điểm của AD và BC chứng minh MN song song với AC.
a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC
Đúng 0
Bình luận (0)
Cho nữa đường tròn tâm O đường kính AB hai tiếp tuyến Ax By M thuộc O tiếp tuyến của nửa đường tròn tại M cắt Ax By ở C và D gọi giao điểm của AD với BC là N MN cắt AB ở I
Chứng minh
a. CD = AC + BD
b. MN song song AC
c. N là trung điểm của MI
Xem chi tiết
a) Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(gt)
CA là tiếp tuyến có A là tiếp điểm(gt)
Do đó: CM=CA(Tính chất hai tiếp tuyến cắt nhau)
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm(gt)
DB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: DB=DM(Tính chất hai tiếp tuyến cắt nhau)
Ta có: CD=CM+DM(M nằm giữa C và D)
mà CM=CA(cmt)
và DM=DB(cmt)
nên CD=CA+DB
Đúng 0
Bình luận (0)
cho nửa đường tròn tâm o đường kính AB.từ A và B kẻ 2 tiếp tuyến Ax By với đường tròn.từ điểm C thuộc đường tròn kẻ tiếp tuyến thứ 3 tiếp tuyến này cắt Ax ở E và By ở F. AC cắt EO tại M, BC cắt OF tại N . chứng minh a) MN song song AB b)MC.OE =EM.Of
Cho Ax, By là các tiếp tuyến song song của đường tròn tâm O. (A,B là các tiếp điểm). Một tiếp tuyến thứ 3 của đường tròn O cắt Ax, By ở M,N. Biết AM=3,2 và BN=5. Tính bán kính của hình tròn.
Cho nửa đường tròn (O) đường kính AB 2R. Trên cùng nửa mặt phẳng bờ AB vẽ hai tiếp tuyến Ax, By. M là điểm trên (O) sao cho tiếp tuyên tại M cắt Ax, By tại D và C. Đường thẳng AD cắt BC tại Na, Chứng minh A, C, M, O cùng thuộc một đường tròn. Chỉ ra bán kính của đường tròn đób, Chứng minh OC và BM song songc, Tìm vị trí điểm M sao cho SACDB nhỏ nhấtd, Chứng minh MN và AB vuông góc nhau
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB = 2R. Trên cùng nửa mặt phẳng bờ AB vẽ hai tiếp tuyến Ax, By. M là điểm trên (O) sao cho tiếp tuyên tại M cắt Ax, By tại D và C. Đường thẳng AD cắt BC tại N
a, Chứng minh A, C, M, O cùng thuộc một đường tròn. Chỉ ra bán kính của đường tròn đó
b, Chứng minh OC và BM song song
c, Tìm vị trí điểm M sao cho SACDB nhỏ nhất
d, Chứng minh MN và AB vuông góc nhau
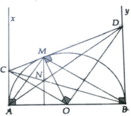
a, Từ CA, CM là tiếp tuyến của (O) chứng minh được A,C,M,O ∈ đường tròn bán kính O C 2
b, Chứng minh OC,BM cùng vuông góc với AM . từ đó suy ra OC//BM
c, S A C D B = A C + B D A B 2 = A D . A B 2
=> S A C D B nhỏ nhất khi CD có độ dài nhỏ nhất
Hay M nằm chính giữa cung AB
d, Từ tính chất hai giao tuyến => AC = CM và BM=MD, kết hợp với AC//BD
ta chứng minh được C N N B = C M M D => MN//BD => MN ⊥ AB
Đúng 0
Bình luận (0)