a) Ta có: AB//CD(gt)

mà E∈AB và F∈CD

nên AE//DF và EB//FC

Xét tứ giác AEFD có AE//DF(cmt)

nên AEFD là hình thang có hai đáy là AE và DF(Định nghĩa hình thang)

Hình thang AEFD(AE//DF) có 

O là trung điểm của EF(gt)

OM//AE//DF(MN//AB//DC, E∈AB, O∈MN, F∈DC)

Do đó: M là trung điểm của AD(Định lí 3 về đường trung bình của hình thang)

Xét tứ giác BEFC có BE//FC(cmt)

nên BEFC là hình thang có hai đáy là BE và FC(Định nghĩa hình thang)

Hình thang BEFC(BE//FC) có 

O là trung điểm của EF(gt)

ON//EB//FC(MN//AB//DC, E∈AB, O∈MN, F∈CD)

Do đó: N là trung điểm của BC(Định lí 3 về đường trung bình của hình thang)

Xét ΔABD có 

M là trung điểm của AD(cmt)

E là trung điểm của AB(gt)

Do đó: ME là đường trung bình của ΔABD(Định nghĩa đường trung bình của tam giác)

⇒ME//BD và NF=BD2NF=BD2(Định lí 2 về đường trung bình của tam giác)(2)

Từ (1) và (2) suy ra ME//NF và ME=NF

Xét tứ giác EMFN có ME//NF(cmt) và ME=NF(cmt)

nên EMFN là hình bình hành(Dấu hiệu nhận biết hình bình hành)

b) Xét ΔBAC có 

E là trung điểm của AB(gt)

N là trung điểm của BC(cmt)

Do đó: EN là đường trung bình của ΔBAC(Định nghĩa đường trung bình của tam giác)

⇒EN//AC và EM=BD2EM=BD2(cmt) và 

a: Xét ΔADC và ΔBCD có

AD=BC

AC=BD

DC chung

Do đó: ΔADC=ΔBCD

Suy ra: \(\widehat{ACD}=\widehat{BDC}\)

hay \(\widehat{ODC}=\widehat{OCD}\)

Xét ΔOCD có \(\widehat{ODC}=\widehat{OCD}\)

nên ΔCOD cân tại O

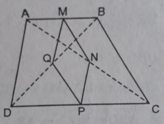
Hình thang ABCD là hình thang cân có hai góc kề một đáy đều bằng 45 0 thì MNPQ là hình vuông.

Xét ΔACD và ΔBDC có 

AC=BD

AD=BC

CD chung

Do đó: ΔACD=ΔBDC

Suy ra: \(\widehat{ODC}=\widehat{OCD}\)

hay OC=OD

a: Xét ΔAOB và ΔCOD có

\(\widehat{OAB}=\widehat{OCD}\)

\(\widehat{AOB}=\widehat{COD}\)

Do đó: ΔAOB\(\sim\)ΔCOD

Suy ra: OA/OC=OB/OD

hay \(OA\cdot OD=OB\cdot OC\)

b: Xét ΔADC có MO//DC

nên MO/DC=AM/AD(1)

Xét ΔBDC có ON//DC

nên ON/DC=BN/BC(2)

Xét hình thang ABCD có MN//AB//CD
nên AM/AD=BN/BC(3)

Từ (1), (2) và (3) suy ra OM=ON

hay O là trung điểm của MN

a)  XÉT HÌNH THANG AEDF(AE//DF) O LÀ TRUNG ĐIỂM EF, OM//DF=> M PHẢI LÀ TĐ CỦA AD

TƯƠNG TỰ C/M N LÀ TĐ BC

ĐẾN ĐÂY LÀM GIỐNG BÀI HÔM TRC ĐÓ E. KẺ 2 ĐƯỜNG CHÉO AC,DB

TAM GIÁC ADB: E,M LÀ TRUNG ĐIỂM 2 CẠNH BÊN => EM LÀ ĐTB => EM//DB. TƯƠNG TỰ VỚI TAM GIÁC DBC:... => FN//DB

=> EM//FN.

TƯƠNG TỰ C/M: EN//MF => TỨ GIÁC EMFN LÀ HÌNH BÌNH HÀNH

B) EMFN LÀ HÌNH THOI <=> EM=EN. MÀ EM=1/2 DB; EN=1/2 AC => AC=DB => HÌNH THANG ABCD CÂN

C) EMFN LÀ HÌNH VUÔNG <=> EMFN LÀ HÌNH THOI (ĐK CÂU B) VÀ EM VUÔNG GÓC EN TẠI E. MÀ EM//DB, EN//AC => DB VUÔNG GÓC AC

=> ABCD là hình thang cân và có 2 đường chéo vuông góc

lần sau kẻ hình nha

123 + 345 = 468

468 + 567 = 1035

1035 - 236 = 799

799 - 189 = 610

610 + 853 = 1463

a / hình bình hành 

b/ AC=BD ; AB>CD ; AB<AC<CD;AB<BD<CD

c/hình vuông

(Hình thì bạn tự vẽ nha)
a) Xét tam giác BAD có: MB=MA ; QB=QD
=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD  (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD                                 (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC                                                        (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN 
=> MNPQ là hình thoi

Do AI, DI lần lượt là phân giác BADˆ;ADCˆ→IADˆ=BADˆ2 và IDAˆ=ADCˆ2

Ta có AIDˆ=180o−(IADˆ+IDAˆ)=180o−BADˆ+ADCˆ2=180o−180o2=90o

Xét Δ AID vuông tại I có IM là trung tuyến thuộc cạnh huyền AD  MA=MI 

=> Δ AMI cân tại M => MAIˆ=MIAˆ

Do MAIˆ=BAIˆ→BAIˆ=MIAˆ

Mà 2 góc ở vị trí so le trong  MI // AB (1)

Tương tự có NJ // AB (2) 

Lại có MN // AB (3) ( MN là đường trung bình của hình thang ABCD ) 

Từ (1); (2) và (3)=>  M, N, I, J thẳng hàng.