logx2 + log2x ≥ \(5/2\)

Những câu hỏi liên quan
Giải bất phương trình
log
x
2
+
1
log
2
x
A.
x
≠
1
B.
x
∈...
Đọc tiếp
Giải bất phương trình log x 2 + 1 > log 2 x
A. x ≠ 1
B. x ∈ R
C. x > 0 x ≠ 1
D. x > 0
Tập nghiệm của bất phương trình
log
2
x
≤
log
x
2
là A.
1
2
;
1
∪
2
;
+
∞
B.
1
2...
Đọc tiếp
Tập nghiệm của bất phương trình log 2 x ≤ log x 2 là
A. 1 2 ; 1 ∪ 2 ; + ∞
B. 1 2 ; 2
C. 0 ; 1 ∪ 1 ; 2
D. 0 ; 1 2 ∪ 1 ; 2
Tập nghiệm của bất phương trình log2x ≤ logx2 là A. B. C. D.
Đọc tiếp
Tập nghiệm của bất phương trình log2x ≤ logx2 là
A. 
B.
C. ![]()
D.
Chọn D
Từ bất phương trình đã cho suy ra:

Phương trình log2(x2 + 2x + 1) = 0 tương đương: x2 + 2x + 1 = 1 hay x2 = 2x = 0
Do đó: x = 0 hoặc x = -2 thỏa mãn điều kiện.
Vậy phương trình có 2 nghiệm.
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình
log
2
x
≤
log
x
2
là
Đọc tiếp
Tập nghiệm của bất phương trình log 2 x ≤ log x 2 là
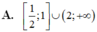
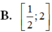
![]()
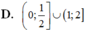
Phương trình
log
x
2
-
7
x
+
12
log
2
x
-
8
có bao nhiêu nghiệm? A. 1 B. 0 C. 2 D. 3
Đọc tiếp
Phương trình log x 2 - 7 x + 12 = log 2 x - 8 có bao nhiêu nghiệm?
A. 1
B. 0
C. 2
D. 3
Phương trình
log
x
2
-
7
x
+
12
log
2
x
-
8
có bao nhiêu nghiệm? A. 1. B. 0. C....
Đọc tiếp
Phương trình log x 2 - 7 x + 12 = log 2 x - 8 có bao nhiêu nghiệm?
A. 1.
B. 0.
C. 2.
D. 3.
Chọn đáp án A
Điều kiện:


Ta có log x 2 - 7 x + 12 = log 2 x - 8
⇔ x 2 - 9 x + 20 = 0

Loại nghiệm x = 4 do không thỏa mãn điều kiện.
Vậy phương trình đã cho có một nghiệm.
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên m để phương trình
log
x
2
-
3
x
+
2
m
log
2
x
+
m
có nghiệm? A. 10. B. 9. C. 8. D. 7.
Đọc tiếp
Có bao nhiêu số nguyên m để phương trình log x 2 - 3 x + 2 m = log 2 x + m có nghiệm?
A. 10.
B. 9.
C. 8.
D. 7.
Gọi
x
1
,
x
2
là hai nghiệm của phương trình
log
2
x
+
log
3
x
.
log
27
-
4
0
. Giá trị của biểu thức
l
o
g
x
1
+
l
o
g
x...
Đọc tiếp
Gọi x 1 , x 2 là hai nghiệm của phương trình log 2 x + log 3 x . log 27 - 4 = 0 . Giá trị của biểu thức l o g x 1 + l o g x 2 bằng
A. 3.
B. -3.
C. -4.
D. 4.
Gọi
x
1
,
x
2
là hai nghiệm của phương trình
log
2
x
+
log
3
x
.
log
27
-
4
0
.Giá trị của biểu thức
log
x
1
+
log
x
2...
Đọc tiếp
Gọi x 1 , x 2 là hai nghiệm của phương trình log 2 x + log 3 x . log 27 - 4 = 0 .Giá trị của biểu thức log x 1 + log x 2 bằng
A. 3
B. -3
C. -4
D. 4












