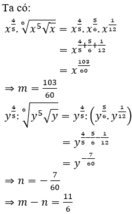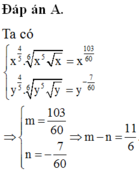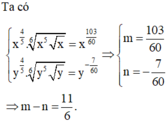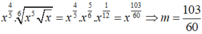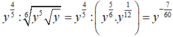khai trien: (xm+yn).(yn-xm)

Những câu hỏi liên quan
Cho x 0; y 0. Viết biểu thức
x
4
5
x
5
x
6
về dạng
x
m
và biểu thức
y
4
5
:
y
5
y...
Đọc tiếp
Cho x > 0; y > 0. Viết biểu thức x 4 5 x 5 x 6 về dạng x m và biểu thức y 4 5 : y 5 y 6 về dạng y n . Ta có x m
A. - 11 6
B. 11 6
C. 8 5
D. - 8 5
Cho
x
0
,
y
0
. Viết biểu thức
x
4
5
.
x
5
x
6
về dạng
x
m
và biểu thức
y
4...
Đọc tiếp
Cho x > 0 , y > 0 . Viết biểu thức x 4 5 . x 5 x 6 về dạng x m và biểu thức y 4 5 . y 5 y 6 về dạng y = y n . Ta có m - n = ?
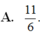
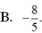
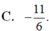
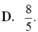
Cho
x
0
,
y
0.
Viết biểu thức
x
4
5
.
x
5
x
6
về dạng
x
m
và biểu thức
y
4
5
.
y...
Đọc tiếp
Cho x > 0 , y > 0. Viết biểu thức x 4 5 . x 5 x 6 về dạng x m và biểu thức y 4 5 . y 5 y 6 về dạng y = y n . Ta có m - n = ?
A. 11 6 .
B. − 8 5 .
C. − 11 6 .
D. 8 5 .
tìm các số nguyên m,n để các đơn thức A và B đồng dạng
Có A =5*xm-3*y2 và B= -0,5*x6*yn
Lời giải:
Để $A,B$ đồng dạng thì: \(\left\{\begin{matrix} m-3=6\\ 2=n\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m=9\\ n=2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho x 0 và y 0. Viết biểu thức
x
4
5
.
x
5
x
6
; về dạng
x
m
và biểu thức
y
4
5
.
y
5
y
6...
Đọc tiếp
Cho x > 0 và y > 0. Viết biểu thức x 4 5 . x 5 x 6 ; về dạng x m và biểu thức y 4 5 . y 5 y 6 về dạng y n . Ta có m – n = ?
A. -11/6
B. 11/6
C. 8/5
D. -8/5
Chứng minh rằng x-y là ước của xm+yn thì x-y cũng là ước của xn+ym(Với x,y,m,n là số nguyên)
a. Vẽ đồ thị (d) của hàm số y=2x
b. Vẽ điểm M ở trên (d) và có hoành độ xM=0.5
Vẽ điểm N ở trên ( d) và có tung độ yN=-2
Tự vẽ, vẽ trên đây khó nhìn
a, Hàm số y=2x
cho x=1 => y= 2
b, Hoành độ
xM=0,5
hay 1.M= 0,5
=> M= 0,5
c, Tung độ yN=-2
hay 2.N=-2
=> N= -1
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn (O) có trung điểm các cạnh AC, AB lần lượt tại M và N. Đường thẳng đi qua A lần lượt vuông góc với AC, AB cắt đường thẳng BC tại X và Y. XM cắt AB tại P, YN cắt AC tại Q. Chứng minh rằng O, P, Q thẳng hàng.
Gọi MO,NO cắt đường thẳng BC lần lượt tại R,S.
Xét \(\Delta XAC\): M là trung điểm cạnh AC, MO || AX vì cùng vuông góc AC, suy ra MO đi qua trung điểm XC
Ta có R là trung điểm XC, MN || XC vì MN là đường trung bình \(\Delta ABC\), suy ra \(M\left(CXRN\right)=-1\)
Tương tự thì \(N\left(YBSM\right)=-1\)
Do đó \(M\left(CXRN\right)=N\left(YBSM\right)\) hay \(M\left(QPON\right)=N\left(QPOM\right)\)
Suy ra P,O,Q thẳng hàng.
Chứng minh tính chất mở rộng của dãy tỉ số bằng nhau:
Nếu \(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}\)
thì ì\(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}=\frac{am-bn+cp}{xm-yn+zp}\)
CM tính chất mở rộng của dãy tỉ số bằng nhau :
Nếu \(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}\) thì \(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}=\frac{am-bn+cp}{xm-yn+zp}\)
Ta có \(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}=\frac{am}{xm}=\frac{bn}{yn}=\frac{cp}{zp}=\frac{am-bn+cp}{xm-yn+zp}\) (đpcm)
Đúng 0
Bình luận (0)