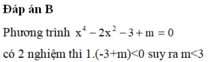Tìm tất cả các giá trị thực của tham số m để bất phương trình -2x2 +2(m-2)x+m-2<0 có nghiệm

Những câu hỏi liên quan
Cho bất phương trình
x
4
+
x
2
+
m
3
-
2
x
2
+
1
3
+
x
2
x
2...
Đọc tiếp
Cho bất phương trình x 4 + x 2 + m 3 - 2 x 2 + 1 3 + x 2 x 2 - 1 > 1 - m (m là tham số). Tìm tất cả các giá trị thực của tham số m để bất phương trình nghiệm đúng với mọi x > 1
A. m > 1
B. m ≥ 1
C. m > 5 4
D. m ≥ 5 4
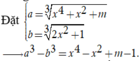
Khi đó bất phương trình trở thành
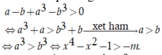
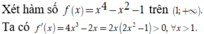
Suy ra hàm số f(x) đồng biến trên ![]()
Do đó yêu cầu bài toán ![]()
Chọn B.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để bất phương trình
2
x
2
+
x
+
2
2
x
+
1
m
có nghiệm trong khoảng
-
∞
;
-
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x 2 + x + 2 2 x + 1 > m có nghiệm trong khoảng - ∞ ; - 1
A. m ∈ - 3 ; + ∞
B. m ∈ [ - 3 ; + ∞ )
C. m ∈ - ∞ ; - 5 2
D. m ∈ ( - ∞ ; - 5 2 ]
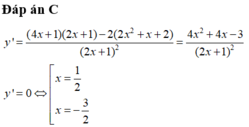
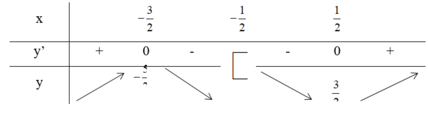
Vậy để bpt có nghiệm trong - ∞ ; - 1 ⇒ m < - 5 2
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để bất phương trình
2
x
2
+
x
+
2
2
x
+
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x 2 + x + 2 2 x + 1 > m có nghiệm trong khoảng − ∞ ; − 1 .
A. m ∈ − 3 ; + ∞ .
B. m ∈ [ - 3 ; + ∞ ) .
C. m ∈ − ∞ ; − 5 2 .
D. m ∈ − ∞ ; - 5 2
Đáp án C
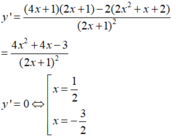
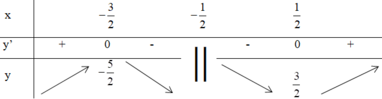
Vậy để bpt có nghiệm trong ( − ∞ ; − 1 ) ⇒ m < − 5 2
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
2
(
x
2
+
m
x
)
-
2
(
2
x
2
+
2
m
x
+
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 ( x 2 + m x ) - 2 ( 2 x 2 + 2 m x + m ) = x 2 +mx+m có nghiệm thực
A. ( - ∞ ; 0 ] ∪ [ 1 ; + ∞ ) .
B. ( - ∞ ; 0 ] ∪ [ 4 ; + ∞ ) .
C. ( - ∞ ; - 1 ] ∪ [ 0 ; + ∞ ) .
D. ( - ∞ ; - 4 ] ∪ [ 0 ; + ∞ ) .
Tìm tất cả các giá trị thực của tham số m để bất phương trình mx^2 + (m-1)x +m -1
Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình
2
x
2
+
2
m
x
+
2
-
2
2
x
2
+
4
m
x
+...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình 2 x 2 + 2 m x + 2 - 2 2 x 2 + 4 m x + m + 2 = x 2 + 2 m x + m có nghiệm thực
A. ( - ∞ , 0 ] ∪ [ 4 , + ∞ )
B. ( 0 , 4 )
C. ( - ∞ , 0 ] ∪ [ 1 , + ∞ )
D. (0,1)
Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình
2
x
2
+
2
m
x
+
2
-
2
2
x
2
+
4
m
x
+...
Đọc tiếp
Tìm tập hợp tất cả các giá trị thực của tham số m để phương trình 2 x 2 + 2 m x + 2 - 2 2 x 2 + 4 m x + m + 2 = x 2 + 2 m x + m có nghiệm thực.
A. ( - ∞ ; 0 ] ∪ [ 4 ; + ∞ ) .
B. ( 0 ; 4 ) .
C. ( - ∞ ; 0 ] ∪ [ 1 ; + ∞ ) .
D. (0;1).
Tìm tất cả các giá trị thực của tham số m để phương trình 4 x 2 − 2 x 2 + 2 + 6 = m có ba nghiệm thực phân biệt?
A. m = 2
B. 2 < m < 3
C. m = 3
D. không tồn tại m
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình
x
4
-
2
x
2
-
3
+
m
0
có đúng 2 nghiệm thực A.
(
-
∞
;
3
)
∪
4
B.
(
-
∞
;
3
)
C.
{
-
4
}
∪
(
-
∞
;...
Đọc tiếp
Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình x 4 - 2 x 2 - 3 + m = 0 có đúng 2 nghiệm thực
A. ( - ∞ ; 3 ) ∪ 4
B. ( - ∞ ; 3 )
C. { - 4 } ∪ ( - ∞ ; 3 )
D. ( - 3 ; + ∞ )