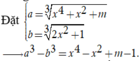
Khi đó bất phương trình trở thành
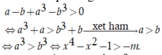
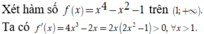
Suy ra hàm số f(x) đồng biến trên ![]()
Do đó yêu cầu bài toán ![]()
Chọn B.
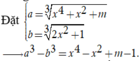
Khi đó bất phương trình trở thành
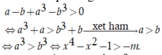
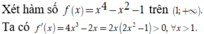
Suy ra hàm số f(x) đồng biến trên ![]()
Do đó yêu cầu bài toán ![]()
Chọn B.
Cho bất phương trình m . 3 x + 1 + ( 3 m + 2 ) ( 4 - 7 ) x + ( 4 + 7 ) x > 0 với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho có nghiệm đúng với mọi x ∈ - ∞ ; 0
A. m ≥ 2 - 2 3 3
B. m > 2 - 2 3 3
C. m > 2 + 2 3 3
D. m ≥ - 2 - 2 3 3
Cho bất phương trình m .3 x + 1 + 3 m + 2 4 − 7 x + 4 + 7 x > 0 , với m là tham số. Tìm tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x ∈ − ∞ ; 0 .
A. m > 2 + 2 3 3 .
B. m > 2 − 2 3 3 .
C. m ≥ 2 − 2 3 3 .
D. m ≥ − 2 − 2 3 3 .
Tìm tất cả các giá trị thực của tham số m để bất phương trình ( m + 1 ) x 2 - 2 ( m + 1 ) x + 4 ≥ 0 ( 1 ) có tập nghiệm S = ℝ ?
A. m > - 1
B. - 1 ≤ m ≤ 3
C. - 1 < m ≤ 3
D. - 1 < m < 3
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
Tìm tất cả các giá trị thực của tham số m để bất phương trình x 2 + 3 x + 3 x + 1 ≥ m nghiệm đúng với mọi x ∈ 0 ; 1
A. m ≥ 3
B. m ≤ 7 2
C. m ≥ 7 2
D. m ≤ 3
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x + 3 + 5 - 2 x ≤ m nghiệm đúng với mọi x ∈ - ∞ ; log 2 5
A. m ≥ 4
B. m < 4
C. m ≥ 2 2
D. m < 2 2
Cho bất phương trình 9 x + ( m - 1 ) 3 x + m > 0 ( 1 ) . Tìm tất cả các giá trị của tham số m để bất phương trình (1) nghiệm đúng ∀ x > 1
A. m ≥ - 3 2
B. m > - 3 2
C. m > 3 + 2 2
D. m ≥ 3 + 2 2
Tìm tất cả các giá trị thực của tham số m để bất phương trình 3 x + 3 + 5 - 3 x ≤ m có nghiệm đúng với mọi x ∈ ( - ∞ ; log 3 5 ]
A. m ≥ 2 2
B. m ≥ 4
C. m ≤ 4
D. m ≤ 2 2
Tìm tất cả các giá tri thực của tham số m để bất phương trình 2 3 x + m − 1 3 x + m − 1 > 0 nghiệm đúng với mọi x ∈ ℝ
A. m ∈ ℝ
B. m > 1
C. m ≤ 1
D. m ≥ 1