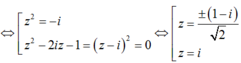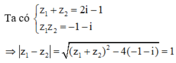GIÚP MÌNH VỚI SOS
Giải phương trình: (z2+i)(z2-2iz-1)=0
Những câu hỏi liên quan
Trong C, phương trình (z2 + i) (z2 – 2iz – 1) 0 có nghiệm là: A. B. 1 - i; -1+ i; 2i C. D. 1 - 2i; -15i; 3i
Đọc tiếp
Trong C, phương trình (z2 + i) (z2 – 2iz – 1) = 0 có nghiệm là:
A. 
B. 1 - i; -1+ i; 2i
C.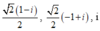 
D. 1 - 2i; -15i; 3i
Giả sử
z
1
,
z
2
là 2 nghiệm phức của phương trình
z
2
+
1
-
2
i
z
-
1
-
i
0
. Khi đó
z
1
-
z...
Đọc tiếp
Giả sử z 1 , z 2 là 2 nghiệm phức của phương trình z 2 + 1 - 2 i z - 1 - i = 0 . Khi đó z 1 - z 2 bằng
A. 3
B. 1
C. 4
D. 2
Phương trình ( z 2 + 1 ) ( z 2 - 2 i z - 1 ) = 0 có bao nhiêu nghiệm?
A. Có 1 nghiệm.
B. Có 2 nghiệm.
C. Có 3 nghiệm.
D. Có 4 nghiệm.
Tìm số phức Z, biết Z là nghiệm của phương trình:
(
2
i
-
1
)
Z
2
-
2
i
Z
¯
+
(
6
+
4
i
)
0
A. Z -i B. Z 1-i C. Z 1+i D. Z i
Đọc tiếp
Tìm số phức Z, biết Z là nghiệm của phương trình: ( 2 i - 1 ) Z 2 - 2 i Z ¯ + ( 6 + 4 i ) = 0
A. Z = -i
B. Z = 1-i
C. Z = 1+i
D. Z = i
Gọi A,B,C là các điểm biểu diễn số phức
z
1
,
z
2
,
z
3
là nghiệm của phương trình
z
z
−
1
−
2
i
z
−
2
+
i
0
....
Đọc tiếp
Gọi A,B,C là các điểm biểu diễn số phức z 1 , z 2 , z 3 là nghiệm của phương trình z z − 1 − 2 i z − 2 + i = 0 . Tính diện tích S của tam giác ABC.
A. 3 2
B. 5
C. 5 2
D. 2
Tính giá trị của biết z1; z2; z3; z4 là nghiệm phức của phương trình ( 5z2 - 6iz - 2)( -3z2+ 2iz) 0. A. 12/25 B. 13/45 C. 11/23 D. 26/7
Đọc tiếp
Tính giá trị của 
biết z1; z2; z3; z4 là nghiệm phức của phương trình ( 5z2 - 6iz - 2)( -3z2+ 2iz) = 0.
A. 12/25
B. 13/45
C. 11/23
D. 26/7
Chọn B.
Phương trình đã cho tương đương với ( -3z2 + 2iz = 0 ( 1) hoặc 5z2 - 6iz - 2 = 0 ( 2)
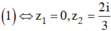
Giải : ta có 
Suy ra 
Do đó: 
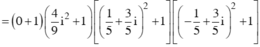
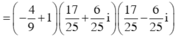
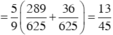
Đúng 0
Bình luận (0)
Giải các phương trình sau: ( z2 + z) 2 + 4( z2+ z) - 12 0 A. z -1; z 2
Đọc tiếp
Giải các phương trình sau: ( z2 + z) 2 + 4( z2+ z) - 12 = 0
A. z = -1; z = 2
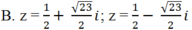
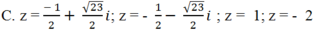
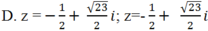
Chọn C.
Đặt t = z2 + z; Phương trình đã cho trở thành
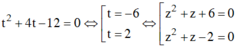
Với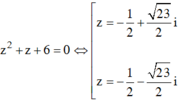 
Với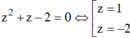 
Vậy phương trình đã cho có 4 nghiệm.
Đúng 0
Bình luận (0)
Tìm số phức z biết
z
2
–
3
+
2
i
z
+
1
+
3
i
0
. A.
z
1
1
+
i
,
z
2
2
-
i
B.
z
1...
Đọc tiếp
Tìm số phức z biết z 2 – 3 + 2 i z + 1 + 3 i = 0 .
A. z 1 = 1 + i , z 2 = 2 - i
B. z 1 = 1 - i , z 2 = 2 + i
C. z 1 = 1 + i , z 2 = 2 + i
D. z 1 = 1 - i , z 2 = 2 - i
Giải các phương trình sau: ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) - 3z2 0 D. Cả A và C đúng
Đọc tiếp
Giải các phương trình sau: ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) - 3z2 = 0
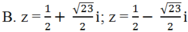
D. Cả A và C đúng
Chọn D.
Ta có: ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) - 3z2 = 0
Hay ( z2 + 3z + 6) 2 + 2z( z2 + 3z + 6) + z2 – 4z2 = 0
[(z2 + 3z + 6) + z]2 - ( 2z)2 = 0
[z2 + 4z + 6 ]2 - ( 2z)2 = 0
Suy ra: (z2 + 4z + 6 - 2z) (z2 + 4z + 6 + 2z) = 0
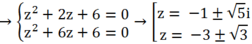
Vậy nghiệm của phương trình là: 
Đúng 0
Bình luận (0)
Biết các số z thỏa mãn:
z
2
-
1
-
2
i
z
-
1
0
. Tính S
z
3
-
1
z
3
A. S 1-2i B. S
1
-...
Đọc tiếp
Biết các số z thỏa mãn: z 2 - 1 - 2 i z - 1 = 0 . Tính S = z 3 - 1 z 3
A. S = 1-2i
B. S = 1 - 2 i 3
C. S = -12i + 27
D. S = -10i