Chọn B.
Phương trình đã cho tương đương với ( -3z2 + 2iz = 0 ( 1) hoặc 5z2 - 6iz - 2 = 0 ( 2)
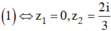
Giải : ta có ![]()
Suy ra ![]()
Do đó: ![]()
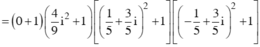
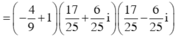
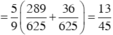
Chọn B.
Phương trình đã cho tương đương với ( -3z2 + 2iz = 0 ( 1) hoặc 5z2 - 6iz - 2 = 0 ( 2)
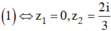
Giải : ta có ![]()
Suy ra ![]()
Do đó: ![]()
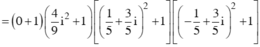
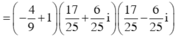
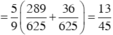
Gọi z 1 , z 2 , z 3 , z 4 là các nghiệm phức của phương trình 2 z 4 - 3 z 2 - 2 = 0 . Tính tổng S = z 1 + z 2 + z 3 + z 4 .
![]()
![]()
![]()
![]()
Kí hiệu z 1 , z 2 , z 3 , z 4 là bốn nghiệm phức của phương trình z 4 - 3 z 2 - 4 = 0 . Tính T = | z 1 + z 2 + z 3 + z 4 |
A. T = 3
B. T = 0
C. T = 4 + 2
D. T = 4
Gọi z 1 , z 2 , z 3 , z 4 là bốn nghiệm phức của phương trình 2 z 4 - 3 z 2 - 2 = 0 . Tổng T = z 1 + z 2 + z 3 + z 4 bằng?
![]()
![]()
![]()
![]()
Gọi z 1 , z 2 , z 3 , z 4 là bốn nghiệm phân biệt của phương trình z 4 + 3 z 2 + 4 = 0 trên tập số phức. Tính giá trị của biểu thức T = z 1 2 + z 2 2 + z 3 2 + z 4 2
A. T = 8
B. T = 6
C. T = 4
D. T = 2
Gọi z 1 , z 2 , z 3 , z 4 là bốn nghiệm phân biệt của phương trình z 4 + 3 z 2 + 4 = 0 trên tập số phức.
Tính giá trị của biểu thức T = z 1 2 + z 2 2 + z 3 2 + z 4 2
A. T=8
B. T=6
C. T=4
D, T=2
Biết z 1 , z 2 , z 3 , z 4 là 4 nghiệm phức của phương trình z 4 + 3 z 2 + 4 = 0 . Tính tổng T = z 1 3 + z 2 3 + z 3 3 + z 4 3 .
A. T = 4(1-i 7 )
B. T = 4(1+i 7 )
C. T = 4
D. T = 0
Biết z 1 , z 2 , z 3 , z 4 là 4 nghiệm phức của phương trình: z 4 - 3 z 2 - 10 = 0 . Tính tổng S = z 1 3 + z 2 3 + z 3 3 + z 4 3
A. T = 4
B. T = 16
C. T = 28
D. T = 58
Gọi z 1 , z 2 , z 3 , z 4 là các nghiệm phức của phương trình z 2 - 4 z 2 - 3 z 2 - 4 z - 40 = 0 . Khi đó, giá trị H = z 1 2 + z 2 2 + z 3 2 + z 4 2 bằng:
![]()
![]()
![]()
![]()
Biết z 1 , z 2 , z 3 , z 4 là bốn nghiệm phức của phương trình 4 z 4 + 3 z 2 + 1 = 0 . Tính tổng T = z 1 2 + z 2 2 + z 3 2 + z 4 2 .
A. T = 4
B. T = 2
C. T = 1
D. T = 0