Bài 13: Cho hình thoi ABCD, biết O là giao điểm của hai đường chéo và góc BAO=40 độ
a) Tính góc BAD
b) Tính các góc còn lại của hình thoi.
Cho hình chóp S. ABCD có đáy ABCD là hình thoi, AB= 2a, góc BAD= 120 độ. Hình chiếu vuông góc của S xuống ( ABCD) trùng với giao điểm I của 2 đường chéo và SI= a/2. Tính góc giữa (SAB) và mặt đáy
1.cho hình thoi ABCD. có góc BAD bằng 40 độ. o là giao điểm của 2 đường chéo H là hình chiếu của O trên AB trên tia dối của tia BC và DC lần lượt lấy M,N sao cho HM//AN. tính góc MON
2. Cho hình vuông ABCD E là tâm của hình vuông. M là trung điểm của AB. Lấy G,H trên BC,CD sao cho MG//AH tính góc GEH
3. Cho hình thang cân ABCD có đáy lớn AB bằng đường chéo AC, đáy nhỏ CD=căn 2 nhân BC.Tính các góc của hình thang ABCD
Gọi O là giao điểm các đường chéo của hình thoi ABCD, E và F theo thứ tự là hình chiếu của O trên BC và CD. Tính các góc của hình thoi biết rằng EF bằng một phần tư đường chéo của hình thoi.
\(nếu ef=1/4 ac thì góc c=a =150 do va goc b=d =30 do neu ef=1/4bd thi goc c=a=120 do va goc b=d=60 do \)
Cho hình thoi ABCD, Ở là giao điểm hai đường chéo. E,F theo thứ twkj là hình chiếu của O trên BC và CD sao cho EF=BD/4. Tính các góc của hình thoi
Một hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình thoi cạnh a, góc B A D ^ = 60 o , cạnh bên hợp với đáy góc 45 o sao cho A’ chiếu xuống mặt phẳng ( ABCD ) trùng với giao điểm O của hai đường chéo mặt đáy. Tính thể tích hình hộp.
A. V = 3 a 3 3 4
B. V = 3 a 3 4
C. V = a 3 3 4
D. V = a 3 4
S A B C D = 2 . a 2 3 4 = a 2 3 2
∆ A A ' O vuông cân ⇒ A ' O = A O = a 3 2
Vậy: V = a 2 3 3 . a 3 3 = 3 a 3 4
Đáp án B
Một hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình thoi cạnh a, góc B A D ⏜ = 60 ∘ , cạnh bên hợp với đáy góc 45 ∘ sao cho A’ chiếu xuống mặt phẳng (ABCD) trùng với giao điểm O của hai đường chéo mặt đáy. Tính thể tích hình hộp.
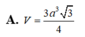
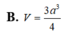
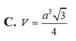
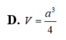
Cho hình thoi ABCD. Gọi O là giao điểm AC và BD. Gọi E, F là hình chiếu của O trên BC, CD. Tính các góc của hình thoi biết rằng EF= 1/4 đường chéo hình thoi.
Mb* giúp H vs ạk ...
Cho hình thoi ABCD, độ dài mỗi cạnh là 13cm. Gọi O là giao điểm hai đường chéo. Vẽ OH vuông góc AD. Biết OH=6cm, tính tỉ số hai đường chéo BD và AC
Bài 1: Cho∆ABC nhọn, H là trực tâm của tam giác. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA; R, S, T lần lượt là trung điểm của HA, HB, HC. CMR: RN=MT=SP.
Bài 2: Gọi O là giao điểm các đường chéo của hình thoi ABCD, E và F theo thứ tự là hình chiếu của O trên BC và CD. Tính các góc của hình thoi biết rằng EF=1/4 các đường chéo của hình thoi.