Hãy điền các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào 9 ô trong bảng:
 |
sao cho thỏa mãn cả hai điều kiện:
 |
| |
Cho 9 số 1 2 3 4 5 6 7 8 9 . Hãy điền mỗi số vào một ô tròn sao cho tổng các số trên mỗi đường kính của đường tròn bằng 15.
tìm tất cả các số tự nhiên n lớn hơn hoặc bằng 3 sao cho có thể đièn các số hữu tỉ vào các ô của bảng ô vuông n*n ô thỏa mãn đồng thời 2 điều kiện sau
điều kiện 1 : tổng các số trong 1 hình vuông 2*2 bất kì là 1 số dương
điều kiện 2 : tổng các số trong 1 hình vuông 3*3 bất kì là 1 số âm
tính xem có bao nhiêu ô vuông
bài 1
cho 7 số -2 ;-4;-5;-6;9;11;7 hãy điền 6 số trên vào đường tròn và 1 số ở tâm đường tròn sao cho được các hàng gồm 3 số thẳng hàng và có tổng bằng nhau và bằng 0
bài 2
cho bảng ô vuông 3x3 ô có thể điền được hay không 9 số nguyên vào 9 ô của bảng sao cho tổng 3 dòng lần lượt là 5;-3;2 và tổng các số ở 3 cột là -1;2;2
Điểm kiểm tra Toán của một lớp được cho trong bảng dưới đây:
| Điểm (x) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Tần số (f) | 0 | 0 | 2 | * | 10 | 12 | 7 | 6 | 4 | 1 | N = * |
trong đó có 2 ô còn trống (thay bằng dấu *). Hãy điền số thích hợp vào ô trống, nếu điểm trung bình của lớp là 6,06.
Gọi x là tần số của điểm 4 (x > 0; x ∈ N)
Số học sinh của lớp:
2 + x + 10 + 12 + 7 + 6 + 4 + 1 = 42 + x
Vì điểm trung bình bằng 6,06 nên:
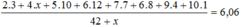
⇔ 6 + 4x + 50 + 72 + 49 + 48 + 36 + 10 = 6,06(42 + x)
⇔ 271 + 4x = 254,52 + 6,06x ⇔ 16,48 = 2,06x
⇔ x = 8 (thỏa mãn điều kiện đặt ra)
Vậy ta có kết quả điền vào như sau:
| Điểm (x) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Tần số (f) | 0 | 0 | 2 | 8 | 10 | 12 | 7 | 6 | 4 | 1 | N = 50 |
Cho bảng vuông 3*3. Người ta điền tất cả các số từ 1 đến 9 vào các ô trong bảng( mỗi số điền 1 ô) sao cho tổng 4 số trên bảng con có kích thước 2*2 đều bằng nhau và bằng số T nào đó. Tìm GTLN của T
Cho một bảng ô vuông 3 × 3
Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng
A. P ( A ) = 10 21
B. P ( A ) = 1 3
C. P ( A ) = 5 7
D. P ( A ) = 1 56
Chọn đáp án C.
Số cách sắp xếp 9 chữ số đã cho vào ô vuông bằng n(Ω)=9!
Ta có: A là biến cố: “tồn tại một hàng hoặc một cột gồm ba số chẵn”.
Do có 4 số chẵn (2, 4, 6, 8) nên A là biến cố: “có đúng một hàng hoặc một cột gồm 3 số chẵn”.
Ta tính n A :
Chọn 4 ô điền số chẵn:
Ø Chọn một hàng hoặc một cột thì có 6 cách.
Ø Chọn một ô còn lại có 6 cách.
Điền 4 số chẵn vào 4 ô trên có 4! cách.
Điền 5 số lẻ vào 5 ô còn lại có 5! Cách.
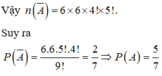
Cho một bảng ô vuông 3 × 3.
Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng
![]()
![]()
![]()
![]()
Cho một bảng ô vuông 3x3
Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của A bằng:
A. P(A) = 1 3
B. P(A) = 5 7
C. P(A) = 1 56
D. P(A) = 10 21
Chọn B
Ta có ![]()
Xét A ¯ : Có ít nhất một hàng hoặc một cột chỉ toàn số chẵn.
Vì chỉ có 4 số chẵn là 2, 4, 6, 8 nên chỉ có thể có đúng một hàng hoặc đúng một cột chỉ toàn các số chẵn. Để điền như vậy cần chọn một trong số ba hàng hoặc ba cột rồi chọn 3 số chẵn xếp vào hàng hoặc cột đó, 6 số còn lại xếp tùy ý. Do đó ![]()
Vậy ![]()
Cho một bảng ô vuông 3x3. Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên ( mỗi ô chỉ điền một số). Gọi A là biến cố: “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của biến cố A bằng:
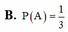
![]()