Cho số nguyên dương n khi đó 2^2 + 4^2+... + (2n)^2 bằng

Những câu hỏi liên quan
2n+4 chia hết cho 2n+2 mà n là số nguyên dương
Ta có 2n+4=(2n+2)+2
Vì 2n+2 chia hết 2n+2 nên 2 chia hết cho 2n+2
Suy ra 2n+2 thuộc ước 2
2n+2 = 1;2
2n = 0;1
n = 0;0,5
Vì n là số nguyên dương nên n=0
Bài 1:Tìm n để: a) \(n^2+2n-4\) chia hết cho 11
b) \(3^{2n+3}+2^{4n+1}\) chia hết cho 25
Bài 2: Tìm số nguyên dương n để 2^n nằm giữa hai số nguyên tố sinh đôi
( 2 số nguyên tố sinh đôi là hai số có hiệu bằng 2)
tìm số nguyên dương n để: (n^2+2n+6)chia hết cho (n+4)
n^2 +2n+6 chia hết cho n+4
tìm nghiệm của bt chia(n+4)
ta tìm được nghiệm là -4
thế nghiệm và bt bị chia
=>(-4)^2+(-4).2+6=14
=.n+4 là ước của 14=(-14,-7,-2,-1,2,7,14)
n+4=-14=>n=-18(loại vì n>0)
n+4=-7=>n=-11(loại)
n+4=-2=>n=-6(loại)
n+4=-1=>n=-5(loại)
n+4=1=>n=-3(loại)
n+4=2=>n=-2(loại)
n+4=7=>n=3(nhận)
n+4=14=>n=10(nhận)
vậy n=3;10
Đúng 0
Bình luận (0)
Cho số nguyên dương n và hệ số của
x
n
-
2
trong khai triển Newton của
x
-
1
4
n
bằng 31.Khi đó n bằng A. 31 B. 33 C. 32 D. 124
Đọc tiếp
Cho số nguyên dương n và hệ số của x n - 2 trong khai triển Newton của x - 1 4 n bằng 31.Khi đó n bằng
A. 31
B. 33
C. 32
D. 124
Chọn C
Ta có:
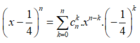
Vì hệ số của x n - 2 trong khai triển Newton của x - 1 4 n bằng 31 nên ta có:
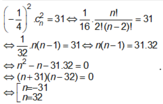
Vì n nguyên dương nên n = 32
Đúng 0
Bình luận (0)
Cho n là số nguyên dương. Chứng minh rằng (2n)!<2^2n.(n!)^2
1. Cho 2 phân số:Y=3n+1/4 và B=18/(n+1)
a, tìm n là số nguyên để YxB là số nguyên dương
b, tìm n để tích hai phân số đã cho bằng -4/1/2.
2. Tìm một bộ 3 số nguyên tố biết rằng trong đó có một số bằng 10% tổng cả 3 số cần tìm.
3. Tìm số dư khi chia 20^10^2013 cho 33.
4. Tìm x,y biết 2^x+3=y^2.
1. Cho 2 phân số:Y=3n+1/4 và B=18/(n+1)
a, tìm n là số nguyên để YxB là số nguyên dương
b, tìm n để tích hai phân số đã cho bằng -4/1/2.
2. Tìm một bộ 3 số nguyên tố biết rằng trong đó có một số bằng 10% tổng cả 3 số cần tìm.
3. Tìm số dư khi chia 20^10^2013 cho 33.
cho n là số dương CMR:
a) 2+4+6+...+2n=n(n+1)
b) 1^3+3^3+5^3+...+(2n-1)^3=2n(2n^2-1)
chứng minh bằng PP quy nạp
a) \(2+4+6+...+2n=n\left(n+1\right)\) (1)
\(n=1\) ta có : \(2=1\cdot\left(1+1\right)\) ( đúng)
Giả sử (1) đúng đến n, ta sẽ chứng minh (1) đúng với n+1
Có \(2+4+6+...+2n+2\left(n+1\right)\)
\(=n\left(n+1\right)+2\left(n+1\right)=\left(n+1\right)\left(n+2\right)\)
=> (1) đúng với n+1
Theo nguyên lý quy nạp ta có đpcm
b) sai đề nha, mình search google thì được như này =))
\(1^3+3^3+5^3+...+\left(2n-1\right)^2=n^2\left(2n^2-1\right)\) (2)
\(n=1\) ta có : \(1^3=1^2\cdot\left(2-1\right)\) (đúng)
giả sử (2) đúng đến n, tức là \(1^3+3^3+...+\left(2n-1\right)^3=n^2\left(2n^2-1\right)\)
Ta c/m (2) đúng với n+1
Có \(1^3+3^3+...+\left(2n+1\right)^3=n^2\left(2n^2-1\right)+\left(2n+1\right)^3\)
\(=2n^4+8n^3+11n^2+6n+1\)
\(=\left(n^2+2n+1\right)\left(2n^2+4n+1\right)\)
\(=\left(n+1\right)^2\left[2\left(n+1\right)^2-1\right]\) => (2) đúng với n+1
Theo nguyên lý quy nạp ta có đpcm
Đúng 1
Bình luận (0)
1/Biết rằng tổng của n số tự nhiên liên tiếp từ 1 n đến bằng 325.Khi đó n=
2/Cho [xo;yo] là các số nguyên dương thỏa mãn: .[x-2][2y+3]=26
Khi đó xo;yo=?















