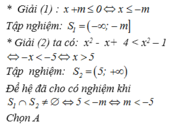Phương trình cos x= m - 4 có nghiệm khi và chỉ khi
Những câu hỏi liên quan
Phương trình m. sin x + 3. cos x = 5 có nghiệm khi và chỉ khi
Cho hệ bất phương trình:
x
+
m
≤
0
x
2
-
x
+
4
x
2...
Đọc tiếp
Cho hệ bất phương trình:
x + m ≤ 0 x 2 - x + 4 < x 2 - 1
Hệ bất phương trình đã cho có nghiệm khi và chỉ khi
A. m < –5
B. m > –5
C. m > 5
D. m < 5
Chọn B.
Xét hệ bất phương trình:
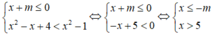
Để hệ bất phương trình có nghiệm thì 5 < -m ⇔ m > -5.
Đúng 0
Bình luận (0)
Cho phương trình: (cos x + 1)( cos 2x – mcos x)m
sin
2
x
. Phương trình có đúng hai nghiệm thuộc đoạn
0
;
2
π
3
khi:
Đọc tiếp
Cho phương trình: (cos x + 1)( cos 2x – mcos x)=m sin 2 x . Phương trình có đúng hai nghiệm thuộc đoạn 0 ; 2 π 3 khi:
Đáp án D
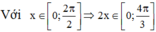
dựa vào đường tròn lượng giác suy ra PT có đúng hai nghiệm khi
Đúng 0
Bình luận (0)
Phương trình
m
+
1
x
2
-
x
-
3
m
+
4
0
có hai nghiệm trái dấu khi và chỉ khi A.
m
-
1
hoặc
m
4
3
B.
m
-
1
hoặc
m
3...
Đọc tiếp
Phương trình m + 1 x 2 - x - 3 m + 4 = 0 có hai nghiệm trái dấu khi và chỉ khi
A. m < - 1 hoặc m > 4 3
B. m < - 1 hoặc m > 3 4
C. m > 4 3
D. - 1 < m < 4 3
Cho hệ bất phương trình
x
+
m
≤
0
1
x
2
-
x
+
4...
Đọc tiếp
Cho hệ bất phương trình x + m ≤ 0 1 x 2 - x + 4 < x 2 - 1 2
Hệ đã cho có nghiệm khi và chỉ khi
A. m<-5
B. m>-5
C. m>5
D. m<5
phương trình x4-(m-1)x2+m-2=0 có hai nghiệm phân biệt khi và chỉ khi nào ?
Phương trình: x + 1 = x + m có 1 nghiệm duy nhất khi và chỉ khi:
A. m = 0
B. m = 1.
C. m = −1.
D. Không tồn tại giá trị m thỏa mãn
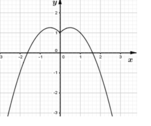
x + 1 = x 2 + m ⇔ m = f x = − x 2 + x + 1 k h i x ≥ 0 − x 2 − x + 1 k h i x < 0
Biểu diễn đồ thị hàm số f(x) lên hệ trục tọa độ như hình vẽ bên trên:
+ Vẽ đồ thị hàm số y = - x 2 + x + 1
+ Giữ nguyên nhánh đồ thị bên phải trục tung và lấy đối xứng nó qua trục tung.
+ Xóa bỏ phần bên trái trục tung trước đó đi.
Dựa vào đồ thị ta suy ra không tồn tại m để phương trình m = f x có duy nhất 1 nghiệm.
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Phương trình x 2 - (m + 1)x + 1 = 0 có nghiệm khi và chỉ khi
A. m > 1
B. –3 < m < 1
C. m ≤ -3 hoặc m ≥ 1
D. -3 ≤ m ≤ 1
Chọn C.
Xét phương trình: x 2 - (m + 1)x + 1 = 0
Ta có: Δ = (m + 1 ) 2 - 4.1.1 = m 2 - 2m + 1 - 4 = m 2 - 2m - 3
Phương trình x 2 - (m + 1)x + 1 = 0 có nghiệm
⇔ Δ ≥ 0 ⇔
m
2
- 2m - 3 ≥ 0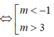 
Đúng 0
Bình luận (0)
Phương trình
x
3
+
x
(
x
+
1
)
m
(
x
2
+
1
)
2
có nghiệm thực khi và chỉ khi: A. m 3/4 B. ¼ m C. m 3 D. Đáp án khác
Đọc tiếp
Phương trình x 3 + x ( x + 1 ) = m ( x 2 + 1 ) 2 có nghiệm thực khi và chỉ khi:
A. m< 3/4
B. ¼< m
C. m> 3
D. Đáp án khác
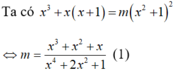
Xét hàm số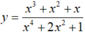 
xác định trên R.
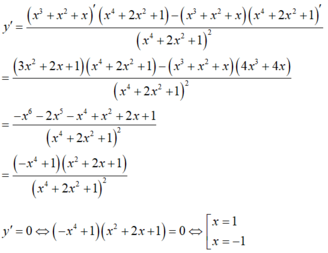
Bảng biến thiên
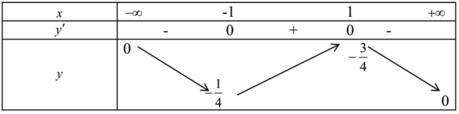
Phương trình (1) có nghiệm thực khi đường thẳng y= m cắt đồ thị hàm số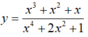 
Khi và chỉ khi -1/4 ≤ m≤ 3/4
Chọn D.
Đúng 0
Bình luận (0)