tìm cạnh huyền, biết đường cao bằng 2.5, hình chiếu 1 cạnh góc vuông bằng 1.5

Những câu hỏi liên quan
Cho hình 36. Hãy viết hệ thức giữa:
a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.
b) Các cạnh góc vuông p, r và đường cao h.
c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'
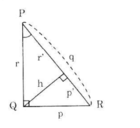
Hình 36
a) p 2 = p ' . q ; r 2 = r ' . q
![]()
c) h 2 = p ' . r '
Đúng 0
Bình luận (0)
Biết tỉ số các cạnh góc vuông của 1 tam giác vuông là 3 : 4.Đường cao ứng với cạnh huyền là 9,6cm.Tính độ dài hình chiếu của mỗi cạnh góc vuông lên cạnh huyền.
Gọi 2 cạnh tam giác vuông là b và c với \(\dfrac{b}{c}=\dfrac{3}{4}\) \(\Rightarrow b=\dfrac{3}{4}c\)
Cạnh huyền là a với \(a=9,6\left(cm\right)\)
Áp dụng định lý Pitago:
\(b^2+c^2=a^2\Rightarrow\left(\dfrac{3}{4}c\right)^2+c^2=\left(9,6\right)^2\)
\(\Rightarrow c=7,68\left(cm\right)\)
\(b=\dfrac{3}{4}c=5,76\left(cm\right)\)
Áp dụng hệ thức lượng:
\(b^2=ab'\Rightarrow b'=\dfrac{b^2}{a}=3,456\left(cm\right)\)
\(c'=a-b'=6,144\left(cm\right)\)
Đúng 0
Bình luận (1)
a) Cho tam giác ABC vuông có tỉ số các cạnh góc vuông bằng k. Tính tỉ số các hình chiếu của hai cạnh góc vuông trên cạnh huyền.
b) Tính độ dài hình chiếu của các cạnh góc vuông trên cạnh huyền của một tam giác vuông, biết rằng tỉ số hai cạnh góc vuông bằng 5:4 và cạnh huyền bằng 82
a/ Kẻ đường cao AH => BH là hình chiếu của AB trên BC và CH là hình chiếu của AC trên BC
Giả sử \(\frac{AB}{AC}=k\Rightarrow\frac{AB^2}{AC^2}=k^2\)
Ta có \(AB^2=BH.BC;AC^2=CH.BC\Rightarrow\frac{AB^2}{AC^2}=\frac{BH}{CH}=k^2\)
b/ Áp dụng câu A sẽ tính được tỷ số hình chiếu 2 cạnh góc vuông trên BC là mà biết chiều dài BC=82 bài toán là dạng tìm 2 số khi biết tổng và tỷ ở lớp 5 rồi bạn tự giải nốt nhé
a)Một tam giác vuông có tỉ số các cạnh góc vuông bằng k. Tính tỉ số các hình chiếu của hai cạnh góc vuông trên cạnh huyền
b) Tính độ dài hình chiếu của các cạnh góc vuông trên cạnh huyền của một tam giác vuông, biết rằng tỉ số hai cạnh góc vuông bằng 5:4 và cạnh huyền dài 82cm
a) Cho tam giác ABC vuông có tỉ số các cạnh góc vuông bằng k. Tính tỉ số các hình chiếu của hai cạnh góc vuông trên cạnh huyền.
b) Tính độ dài hình chiếu của các cạnh góc vuông trên cạnh huyền của một tam giác vuông, biết rằng tỉ số hai cạnh góc vuông bằng 5:4 và cạnh huyền bằng 82
Help me please
Cho tam giác vuông có tỉ số giữa một cạnh góc vuông và cạnh huyền bằng \(\frac{3}{5}\). Cạnh góc vuông còn lại dài 12 cm. Tính độ dài đường cao, độ dài hình chiếu của hai cạnh góc vuông lên cạnh huyền.
Đặt \(\frac{AB}{BC}=\frac{3}{5}=x\Rightarrow AB=3x;BC=5x\)
Tam giác ABC vuông tại A, theo py ta go:
\(AB^2+AC^2=BC^2\Rightarrow9x^2+144=25x^2\Rightarrow16x^2=144\Leftrightarrow x^2=9\)
=> X = 3 ; AB = 3x = 3.3=9 ; BC= 5x = 5.3 = 15
TAm giac ABC vuông tại A theo hệ thức lượng
AH.BC = AB.AC => AH= (AB.AC)/BC = (9.12)/15 = 7,2cm
AB^2 = BC . BH => BH = AB^2 /BC = 9^2/15 = 5,4
=> HC = BC - HB = 15 - 5,4 = 9,6cm
VẬY AH = 7,2 ; BH = 5,4;CH = 9,6
Đúng 0
Bình luận (0)
Biết tỉ số các cạnh góc vuông của một tam giác vuông là 3:7 ; đường cao ứng với cạnh huyền là 12cm. Tính độ dài hình chiếu của mỗi cạnh góc vuông lên cạnh huyền
Hình 1 tìm x,y,z là 2 cạnh góc vuông với đg cao. Biết cạnh huyền bằng 9
Bạn cho mình xin hình vẽ nha bạn
Đúng 0
Bình luận (3)
Biết tỉ số hai cạnh góc vuông của một tam giác vuông là 3 : 7 , đường cao ứng với cạnh huyền là 42 cm . Tính độ dài hình chiếu của các cạnh góc vuông trên cạnh huyền . Help me plz
Gọi 2 cạnh góc vuông là `AB,AC`, cạnh huyền là `BC`, đường cao `AH`.
Có: `(AB)/(AC)=3/7 = (3x)/(7x) (x>0)`
Áp dụng hệ thức lượng trong tam giác vuông ABC:
`1/(AH^2)=1/(AB^2)+1/(AC^2)`
`<=>1/(42^2)=1/(9x^2)+1/(49x^2)`
`=> x=2\sqrt58(cm)`
`=> AB=6\sqrt58, AC=14\sqty58 (cm)`
Áp dụng định lí Pytago:
`AB^2=HB^2+AH^2`
`<=> (6\sqrt58)^2=HB^2+42^2`
`=> HB=18(cm)`
`=> HC = AH^2 : HB = 98(cm)`
Vậy `HB=18cm, HC=98cm`.
Đúng 1
Bình luận (4)



















