Ai chỉ cách giải phương trình bậc 4 với.
Ko dùng máy tính.
Có ai biết cách giải các phương trình tích có bậc cao như bậc 5,6 không.Ai biết chỉ với mình kich cho
AxBx = 0 thi tim nghiem cua A va B roi giai binh thuong
chuyển hết về qua 1 bên còn về bên kia = 0 sau đó rút gọn rồi đặt nhân tử chung ra và giải như phương trình tích là đc
Nêu cách giải phương trình bậc 4
a x a = 676, a bằng mấy. trình bày cách giải nha :) chưa học căn bậc 2 hay bình phương nên chỉ được giải theo chương trình lớp 5
Lời giải:
Vì 2 số giống nhau nhân với nhau có tận cùng là 6 nên $a$ có tận cùng là $6$.
$a\times a=676$ nên $a$ là số có 2 chữ số.
Đặt $a=\overline{x6}$ với $x$ là số tự nhiên có 1 chữ số, $x>0$.
Ta có:
$\overline{x6}\times \overline{x6}=676$
$(10\times x+6)(10\times x+6)=676$
$100\times x\times x+120\times x+36=676$
$100\times x\times x+120\times x=640$
$10\times x\times x+12\times x=64$
$5\times x\times x+6\times x=32$
$x\times (5\times x+6)=32$
Vì $x\geq 1$ nên:
$32=x\times (5\times x+6)\geq x\times 11$
$32:11\geq x$
$2,9\geq x$
$\Rightarrow x=1$ hoặc $x=2$
Nếu $x=1$ thì: $x\times (5\times x+6)=1\times (5\times 1+6)=11$ (loại)
Nếu $x=2$ thì $2\times (5\times 2+6)=32$ (thỏa mãn)
Vậy $x=2$
Tức $a=26$.
Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: 4 x 2 – 12x + 5 = 0
4 x 2 – 12x + 5 = 0 ⇔ 4 x 2 – 2x – 10x + 5 = 0
⇔ 2x(2x – 1) – 5(2x – 1) = 0 ⇔ (2x – 1)(2x – 5) = 0
⇔ 2x – 1 = 0 hoặc 2x – 5 = 0
2x – 1 = 0 ⇔ x = 0,5
2x – 5 = 0 ⇔ x = 2,5
Vậy phương trình có nghiệm x = 0,5 hoặc x = 2,5
có ai bk cách dùng Công thức Newton dùng để tìm nghiệm của phương trình
chỉ m,k với!
a^n-b^n= (a-b).(.......) với mọi n
Dùng công thức Niu tơn để tìm nghiệm của pt thì (a-b) chính là nghiệm đó bạn
Giải phương trình bậc 3 bằng cách dùng pp cardano sau :
\(x^3-3x^2+4x+11=0\)
giúp mình câu này thôi do câu này nghiệm căn bậc 3
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
3x2 + 5x + 2 = 0
Phương trình bậc hai 3x2 + 5x + 2 = 0
Có a = 3; b = 5; c = 2; Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
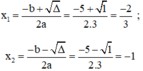
Vậy phương trình có hai nghiệm là -1 và 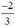
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
y2 – 8y + 16 = 0
Phương trình bậc hai y2 – 8y + 16 = 0
Có a = 1; b = -8; c = 16; Δ = b2 – 4ac = (-8)2 – 4.1.16 = 0.
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :
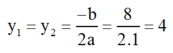
Vậy phương trình có nghiệm kép y = 4.
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
6x2 + x + 5 = 0
Phương trình bậc hai 6x2 + x + 5 = 0
Có a = 6; b = 1; c = 5; Δ = b2 – 4ac = 12 – 4.5.6 = -119 < 0
Vậy phương trình vô nghiệm.