Tam giác ABC, \(\widehat{BAC}\)=75 độ, đường cao AH, BH=\(\sqrt{3}\)CH. Chứng minh AH=BH, tính số đo \(\widehat{ABC},\widehat{ACB}\)

Những câu hỏi liên quan
cho tam giác abc vuông a có đường cao ah biết ah 6cm,ch 9cm tính bh,ab,widehat{acb}(kết quả làm tròn đến độ),gọi d,e lần lượt là hình chiếu của h trên ab,ac.chứng minh frac{bd}{ab}frac{ce}{ac}1.bdsqrt{ch}+cesqrt{bh}ahsqrt{bc}cho tam giác abc vuông a có ab 3cm,ac 4cm,đc ah. tính bc,ah.tính widehat{b},widehat{c}.phân giác của góc a cắt bc tại e.tính be,cegiúp mk nhé
Đọc tiếp
cho tam giác abc vuông a có đường cao ah biết ah 6cm,ch 9cm tính bh,ab,\(\widehat{acb}\)(kết quả làm tròn đến độ),gọi d,e lần lượt là hình chiếu của h trên ab,ac.chứng minh \(\frac{bd}{ab}=\frac{ce}{ac}=1\).\(bd\sqrt{ch}+ce\sqrt{bh}=ah\sqrt{bc}\)
cho tam giác abc vuông a có ab 3cm,ac 4cm,đc ah. tính bc,ah.tính \(\widehat{b}\),\(\widehat{c}\).phân giác của góc a cắt bc tại e.tính be,ce
giúp mk nhé
cho tam giác ABC cân tại A , đường cao AH , biết AB = 5cm , BC = 6cm
a, Tính độ dài đoạn thẳng BH , AH
b, Gọi G là trọng tâm của tam giác ABC , Chứng minh : A , G , H thẳng hàng
c, chứng minh : \(\widehat{ABG}=\widehat{ACG}\)
em ko biet lam moi chi hoc lop 5 thoi
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, AH là đường cao.
a/Chứng minh \(AB^2+CH^2=AC^2+BH^2\)
b/Gọi M, N theo thứ tự là hình chiếu của H trên AB và AC. Chứng minh \(\widehat{AMN}=\widehat{ACB}\)
cho tam giác abc có đường cao ah biết bc8cm ab\(4+2\sqrt{3}\)cm và \(\widehat{abc}\)=60 độ tính bh,ac
cho tam giác ABC vuông tại A có đường cao AH. Biết AB=6.a, AC=8.a, với a là số thực dương
a) Tính AH,BH,CH theo a.
b) Tính tan\(\widehat{ACB}\)
Bài 4: Cho tam giác ABC (AB AC), đường cao BH. Từ điểm D thuộc cạnh BC kẻ DE ⊥ AB (E ∈ AB); DF ⊥ AC (F ∈ AC) và DK ⊥ BH (K ∈ BH)a) Chứng minh: widehat{KDB}widehat{ACB}b) Chứng minh: ΔEBD ΔKDB.c) Chứng minh: DE + DF BH.d) Trên tia đối của tia CA lấy điểm P sao cho CP HF. Chứng minh rằng trung điểm của EP nằm trên BC.e) Cho widehat{A}40^o, kẻ đường cao AH. Trên các đoạn thẳng AH, AC lấy thứ tự các điểm E, F sao cho widehat{ABE}widehat{CBF}30^o. Tính góc AEF.
Đọc tiếp
Bài 4: Cho tam giác ABC (AB = AC), đường cao BH. Từ điểm D thuộc cạnh BC kẻ DE ⊥ AB (E ∈ AB); DF ⊥ AC (F ∈ AC) và DK ⊥ BH (K ∈ BH)
a) Chứng minh: \(\widehat{KDB}=\widehat{ACB}\)
b) Chứng minh: ΔEBD = ΔKDB.
c) Chứng minh: DE + DF = BH.
d) Trên tia đối của tia CA lấy điểm P sao cho CP = HF. Chứng minh rằng trung điểm của EP nằm trên BC.
e) Cho \(\widehat{A}=40^o\), kẻ đường cao AH. Trên các đoạn thẳng AH, AC lấy thứ tự các điểm E, F sao cho \(\widehat{ABE}=\widehat{CBF}=30^o\). Tính góc AEF.
Cho tam giác ABC có \(\widehat{C}\)=2\(\widehat{B}\),đường cao AH .
Chứng minh : a, AC+CH=BH
b, \(^{AB^2}\)> AC.BC
làm câu a thôi nha
a) trên tia HB lấy HK sao cho HK = HC
xét tam giác ACH và tam giác AKH có :
AH ( cạnh chung )
\(\widehat{AHC}=\widehat{AHK}=90^o\)
HC = HK ( theo cách vẽ )
suy ra : tam giác ACH = tam giác AKH ( c.g.c )
=> HC = HK ( hai cạnh tương ứng )
=> \(\widehat{C}=\widehat{AKH}\)( hai góc tương ứng )
=> AC = AK ( hai cạnh tương ứng )
tam giác AKB có \(\widehat{AKH}\)là góc ngoài tại đỉnh K có :
\(\widehat{AKH}\)= \(\widehat{KAB}+\widehat{B}\)
Mà \(\widehat{C}=2.\widehat{B}\)hay \(\widehat{AKH}\)= \(2.\widehat{B}\)
\(\Rightarrow2.\widehat{B}=\widehat{KAB}+\widehat{B}\)
\(\Rightarrow\widehat{KAB}=\widehat{B}\)
=> tam giác KAB cân tại K
=> KA = KB
=> AC + CH = KB + HK = BH
b)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có \(\widehat {ABC} = 70^\circ \). Hai đường cao BD và CE cắt nhau tại H.
a) Tính số đo các góc còn lại của tam giác ABC.
b) Chứng minh BD = CE.
c) Chứng minh tia AH là tia phân giác của góc BAC.
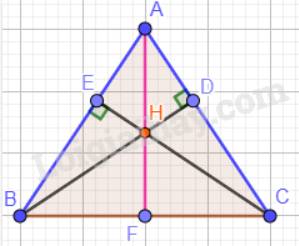
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).
Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ - 70^\circ - 70^\circ = 40^\circ \).
b) Xét tam giác vuông ADB và tam giác vuông AEC có:
AB = AC (tam giác ABC cân);
\(\widehat A\) chung.
Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).
c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.
Xét hai tam giác vuông AFB và AFC có:
AB = AC (tam giác ABC cân);
AF chung.
Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).
Vậy tia AH là tia phân giác của góc BAC.
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, có đường cao AH; BH = 4cm, CH= 9cm. Từ H kẻ HD vuông góc AB, HE vuông góc AC.
a. Tính AH
b. Chứng minh: tam giác ADE đồng dạng với tam giác ACB
c. Kẻ đường thẳng vuông góc với DE tại E, cắt HC tại M. Tính \(\sin\widehat{DME}\)













