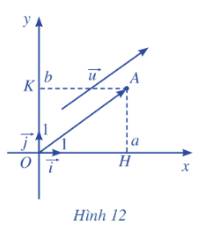
Trong mặt phẳng toạ độ Oxy, cho vectơ\(\overrightarrow u {\rm{ }} = {\rm{ }}\left( {a;{\rm{ }}b} \right)\) . Ta chọn điểm A sao cho\(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) . Xét vectơ đơn vị \(\overrightarrow i \) trên trục hoành Ox và vectơ đơn vị \(\overrightarrow j \) ở trên trục tung Oy (Hình 12).
a) Tìm hoành độ và tung độ của điểm A.
b) Biểu diễn vectơ OH qua vectơ \(\overrightarrow i \).
c) Biểu diễn vectơ OK qua vecto \(\overrightarrow j \).
d) Chứng tỏ rằng\(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \)