S = 2. 10 + 2. 12 + 2. 14 + … + 2. 20 cứu mấy ní tui mới lên lớp 6
Những câu hỏi liên quan
S= 2^2+4^2+6^2+8^2+10^2+12^2+14^2+16^2+18^2+20^2
Tính S= 2^2-4^2+6^2-8^2+10^2-12^2+14^2-16^2+18^2-20^2
1,tính nhanh
A1.3+3.5+5.7+...+97.99
2,Trong đợt thi đua lớp 6a có 35 bạn đạt 1 ddieerm10 trở lên, 28 bạn đạt 2 điểm 10 trở lên.9 bạn đạt 4 điểm 10,không bạn nào đạt trên 4 điểm 10.hỏi lớp 6a trong đợt thi đua đó đạt được bao nhiêu điểm 10?
3, đổi 185 sang hệ cơ số 5
đổi 2434(6) sang hệ cơ số 9
4,S2+2^2+2^3+...+2^100
chứng minh :Schia hết cho 6 ,S chia hết cho 14, Schia hết cho 30, Schia hết cho31
5,tìm x thuộc z:
2x-5 chia hết cho 6-x
(x-1).(y-2)9
x.y180,BCNN(x,y)20(x,y)
ĐỀ KIỂM TRA 4...
Đọc tiếp
1,tính nhanh
A=1.3+3.5+5.7+...+97.99
2,Trong đợt thi đua lớp 6a có 35 bạn đạt 1 ddieerm10 trở lên, 28 bạn đạt 2 điểm 10 trở lên.9 bạn đạt 4 điểm 10,không bạn nào đạt trên 4 điểm 10.hỏi lớp 6a trong đợt thi đua đó đạt được bao nhiêu điểm 10?
3, đổi 185 sang hệ cơ số 5
đổi 2434(6) sang hệ cơ số 9
4,S=2+2^2+2^3+...+2^100
chứng minh :Schia hết cho 6 ,S chia hết cho 14, Schia hết cho 30, Schia hết cho31
5,tìm x thuộc z:
2x-5 chia hết cho 6-x
(x-1).(y-2)=9
x.y=180,BCNN(x,y)=20(x,y)
ĐỀ KIỂM TRA 45 PHUT CHIỀU CỦA MÌNH ĐẤY!NGỒI SUỐT 2 TIẾNG MÀ MỚI LÀM ĐƯỢC VÀI BÀI.
2-4+6-8+10-12+14-16+18-20+22
tính nhanh nha
(lớp 3 đó,giải theo cách lớp 3)
Xem thêm câu trả lời
d) S = 2. 10 + 2. 12 + 2. 14 + … + 2. 20
d) $S=2\cdot10+2\cdot12+2\cdot14+\dots+2\cdot20$
$=2\cdot(10+12+14+\dots+20)$
Đặt: $A=10+12+14+\dots+20$
Số các số hạng của $A$ là:
$(20-10):2+1=6$ (số)
Tổng $A$ bằng:
$(20+10)\cdot6:2=90$
Thay $A=90$ vào $S$, ta được:
$S=2\cdot90=180$
Đúng 2
Bình luận (0)
26 tháng 10 2023 lúc 20:02
a.2/3+2/6+2/12+2/24+2/48+2/96+2/192
cứu tui
\(\dfrac{2}{3}+\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{24}+\dfrac{2}{48}+\dfrac{2}{96}+\dfrac{2}{192}\\ =\dfrac{128}{192}+\dfrac{64}{192}+\dfrac{32}{192}+\dfrac{16}{192}+\dfrac{8}{192}+\dfrac{4}{192}+\dfrac{2}{192}\\ =\dfrac{128+64+32+16+8+4+2}{192}\\ =\dfrac{254}{192}=\dfrac{127}{96}\)
Đúng 1
Bình luận (0)
a, 47 -[ [ 45 . 24 - 52. 12 ] :14]
b, 50- [[20-23 ] :2 + 34 ]
c, 102 - [[ 60:[52:54- 3.5 ]
d, 50- [[ 50- 23.5 ]:2 +3]
cái dấu chấm là nhân đấy các bạn lên lớp 6 các bạn sẽ học nhé làm hộ mình nhé cố lên
a.=47-[45.16-25.12]:14]
=47-420:14
=47-30
=17
b.=50-[12:2+34]
=50-40
=10
c.=100-60:10
=100-6
=94
d.50-[(50-40);2+3]
=50-(10:2+3)
=50-8
=42
Đúng 0
Bình luận (0)
1+2-4+6-8+10-12+.............+2010-2012+2013
9/10+1/90+1/72+1/56+1/42+1/30+1/20+1/12+1/6+1/2
tính giúp tui với thứ 6 tui nộp zùi và tick lẫn kb với tui nhé
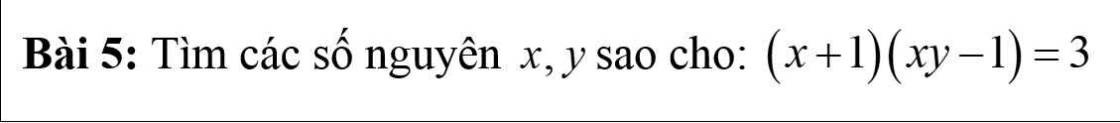
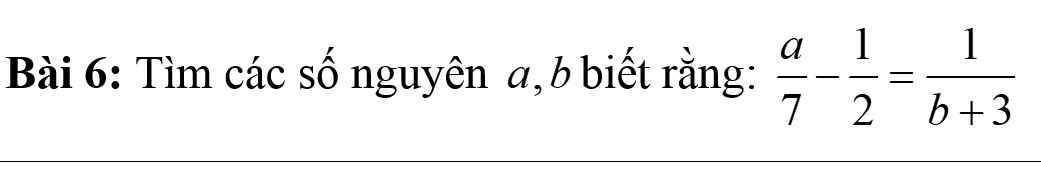
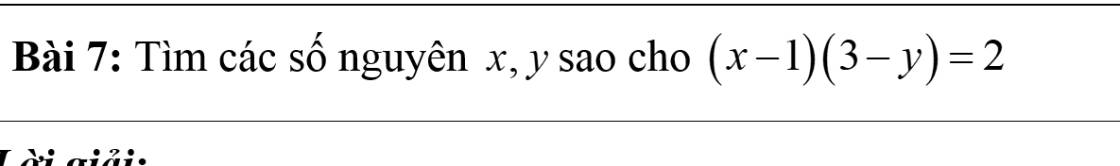cứu mik mấy ní oi
Bài 5:
Với $x,y$ là số nguyên thì $x+1, xy-1$ cũng là số nguyên. Mà tích của chúng bằng 3 nên ta có các TH sau:
TH1: $x+1=1, xy-1=3\Rightarrow x=0; xy=3$ (vô lý - loại)
TH2: $x+1=-1, xy-1=-3\Rightarrow x=-2; xy=-2\Rightarrow y=1$ (thỏa mãn)
TH3: $x+1=3; xy-1=1\Rightarrow x=2; xy=2\Rightarrow y=1$ (thỏa mãn)
TH4: $x+1=-3; xy-1=-1\Rightarrow x=-4; xy=0$ (vô lý -loại)
Vậy......
Đúng 0
Bình luận (0)
Bài 6:
$\frac{a}{7}-\frac{1}{2}=\frac{1}{b+3}$
$\Rightarrow \frac{2a-7}{14}=\frac{1}{b+3}$
$\Rightarrow (2a-7)(b+3)=14$
Với $a,b$ nguyên thì $2a-7, b+3$ cũng là số nguyên. Mà $(2a-7)(b+3)=14$ và $2a-7$ là số nguyên lẻ nên ta các TH sau:
TH1: $2a-7=1; b+3=14\Rightarrow a=4; b=11$ (thỏa mãn)
TH2: $2a-7=-1; b+3=-14\Rightarrow a=3; b=-17$ (thỏa mãn)
TH3: $2a-7=7; b+3=2\Rightarrow a=7; b=-1$ (thỏa mãn)
TH4: $2a-7=-7; b+3=-2\Rightarrow a=0; b=-5$ (thỏa mãn)
Đúng 0
Bình luận (0)
Bài 7:
Với $x,y$ nguyên thì $x-1, 3-y$ cũng nguyên. Mà $(x-1)(3-y)=2$ nên ta có các TH sau:
TH1: $x-1=1, 3-y=2\Rightarrow x=2; y=1$ (thỏa mãn)
TH2: $x-1=-1; 3-y=-2\Rightarrow x=0; y=5$ (thỏa mãn)
TH3: $x-1=3; 3-y=1\Rightarrow x=4; y=2$ (thỏa mãn)
TH4: $x-1=-3; 3-y=-1\Rightarrow x=-2; y=4$ (thỏa mãn)
Đúng 0
Bình luận (0)