2. không tính kết quả, hay so sánh:
a) A= 2022.2024 và B= 20232
Hãy thực hiện các phép tính sau :
a, x y : y z
b, y z : x y
c, x y : y z : z x
d, x y : y z : z x
So sánh kết quả của a với kết quả của b; kết quả của c với kết quả của d
Phép chia có tính chất giao hoán và tính chất kết hợp hay không ?
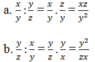
Kết quả câu b là nghịch đảo kết quả câu a.
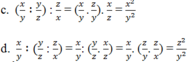
Kết quả câu c và d khác nhau. Phép chia không có tính chất giao hoán, tính chất kết hợp.
Ko tính giá trị cụ thể hãy so sánh
b) c = 25 . 26261 và d = 26. 25251
c) a= 2023 . 2023 và b = 2022.2024
a)
Ta có:
\(c=25\times26261=25\times\left(26260+1\right)=25\times10\times26\times101+25\)
\(d=26\times25251=26\times\left(25250+1\right)=26\times10\times25\times101+26\)
Vì \(25\times10\times26\times101\) = \(26\times10\times25\times101\) mà \(25< 26\)
=> \(c< d\)
b)
Ta có:
\(b=2022\times2024=2022\times\left(2023+1\right)=2022\times2023+2022\)
\(a=2023\times2023=2023\times\left(2022+1\right)=2023\times2022+2023\)
Vì \(2022\times2023=2023\times2022\) mà \(2022< 2023\)
=> \(b< a\)
So sánh A và B mà không cần tính ra kết quả cụ thể [viết ra cách làm để so sánh sao cho không cần tính ra kết quả :
a, A = 1998.1998 ; B= 1996.2000
b, A= 25.33-10 ; B= 31.26+10
a)A=(1996+2).(2000-2)
A=1996.2000-1996.2+2000.2-4
A=1996.2000+4
=>A>B
A=(26-1).(31+2)-10
A=26.31+2.26-31-2-10
A=26.31+9
A<B
2. không tính kết quả, hay so sánh:
b) M= \(\dfrac{10^{2023}+1}{10^{2024}+1}\) và N= \(\dfrac{10^{2022}+1}{10^{2023}+1}\)
b) \(M=\dfrac{10^{2023}+1}{10^{2024}+1}< 1\) ( Vì tử < mẫu )
Ta có: \(M=\dfrac{10^{2023}+1}{10^{2024}+1}< \dfrac{10^{2023}+1+9}{10^{2024}+1+9}=\dfrac{10^{2023}+10}{10^{2024}+10}=\dfrac{10.\left(10^{2022}+1\right)}{10.\left(10^{2023}+1\right)}=\dfrac{10^{2022}+1}{10^{2023}+1}=N\)
Vì \(\dfrac{10^{2023}+1}{10^{2024}+1}< \dfrac{10^{2022}+1}{10^{2023}+1}\) nên \(M< N\)
Không tính kết quả hãy so sánh A và B: A=1999x1999 và B=1997x2001
Bạn trình bày bài giải cho mình nhé
Ta có:
\(A=1999\times1999=1999\times\left(1997+2\right)=1999\times1997+1999\times2\)
\(B=1997\times2001=1997\times\left(1999+2\right)=1999\times1997+1997\times2\)
Vì \(1999\times1997+1999\times2>1999\times1997+1997\times2\)Nên \(A>B\)
cho a=2011.2013 và b=2012.2012 không tính kết quả hãy so sánh a và b
a = 2011.2013
a = 2011.(2012+1)
a = 2011.2012 + 2011
b = 2012.2012
b = (2011+1).2012
b = 2011.2012 + 2012
Vì 2011 < 2012
=> 2011.2012 + 2011 < 2011.2012 + 2012
=> a < b
Cho A = 2013.2013 và B = 2014.2012. Không tính kết quả hãy so sánh A và B
3. So sánh A và B mà không tính kết quả cụ thể: A = 20202
và B = 2018. 2022
\(B=2018.2022=\left(2020-2\right)\left(2020+2\right)=2020^2-2.2020+2.2020-2.2\)
\(=A-4< A\).
So sánh hai số A và B mà không tính kết quả cụ thể A=20132 và B=2012.2014
A= 2013. ( 2021 + 1 ) = 2013 . 2012 + 2013
B = 2012 . 2014 = 2012 . ( 2013 + 1 ) = 2012 . 2013 + 2012
Vì 2013 > 2012 ==> A > B