cho 4 tam giác ABC hãy vẽ ở mỗi tam giác các đường trung tuyến AM đường phân giác AI đường cao AH đường trung trực ứng với BC

Những câu hỏi liên quan
Cho tam giác ABC vuông ở A . Vẽ đường cao AH . Trung tuyến AM . Kẻ đường phân giác góc A cắt đường trung trực cạnh BC tại D . Từ D kẻ DE vuông góc với AB tại D , DF vuông góc với AC tại F
a) CM : AD là phân giác góc HAM
b) CM : 3 điểm E , M , F thẳng hàng
c) CM : Tam giác BDC vuông cân
Cho tam giác ABC vuông tại A đường cao AH Đường trung tuyến AM
a) Hãy chỉ ta các điểm là trọng tâm ,trực tâm giữa 3 đường trung trực của tam giác ABC
b) cho AB=16 cm AC=12 cm Tính AH;AM;MH
Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác trong AD, đường trung tuyến AM.
a;Chưng minh HD+DM=HM
b; Vẽ các đường cao BF, CE. So sánh hai đoạn thẳng BF và CE
c CM tam giác AFE~tam giác ABC
d; Gọi O là trực tâm của tam giác ABC. Chứng minh BO.BF+CO.CE=BC^2
Giups mk câu d với ạ
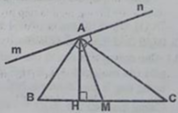
Cho tam giác ABC vuông ở A, AH và AM tương ứng là đường cao và đường trung tuyến kẻ từ A của tam giác đó. Qua điểm A kẻ đường thẳng mn vuông góc với AM. Chứng minh: AB và AC tương ứng là tia phân giác của các góc tạo bở AH và hai tia Am, An của đường thẳng mn.
Cho tam giác ABC vuông tại A, kẻ đường cao AH và trung tuyến AM. đường phân giác góc A, cắt đường trung trực BC tại D. Từ D kẻ DE vuông góc với BA và DF vuông góc với AC.
a, CMR: AD là phân giác góc HAM
b, 3 điểm E, M, F thẳng hàng
c, Tam giác ABC là tam giác vuông cân
Cho tam giác ABC vuông tại A, kẻ đường cao AH và trung tuyến AM. đường phân giác góc A, cắt đường trung trực BC tại D. Từ D kẻ DE vuông góc với BA và DF vuông góc với AC.
a, CMR: AD là phân giác góc HAM
b, 3 điểm E, M, F thẳng hàng
c, Tam giác ABC là tam giác vuông cân
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH 4cm, CH 9cm.a) Tính độ dài đường cao AH và
A
B
C
⏜
của tam giác ABC.b) Vẽ đường trung tuyến AM
M
∈
B
C
của tam giác ABC, tính AM và diện tích tam giác AHM
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH= 4cm, CH= 9cm.
a) Tính độ dài đường cao AH và A B C ⏜ của tam giác ABC.
b) Vẽ đường trung tuyến AM M ∈ B C của tam giác ABC, tính AM và diện tích tam giác AHM

a , Δ A B C , A ⏜ = 90 0 , A H ⊥ B C g t ⇒ A H = B H . C H = 4.9 = 6 c m Δ A B H , H ⏜ = 90 0 g t ⇒ tan B = A H B H = 6 4 ⇒ B ⏜ ≈ 56 , 3 0 b , Δ A B C , A ⏜ = 90 0 , M B = M C g t ⇒ A M = 1 2 B C = 1 2 .13 = 6 , 5 c m S Δ A H M = 1 2 M H . A H = 1 2 .2 , 5.6 = 7 , 5 c m 2
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông ở A, AH và AM tương ứng là đường cao và đường trung tuyến kẻ từ A của tam giác đó. Qua điểm A kẻ đường thẳng mn vuông góc với AM.
Chứng minh : AB và AC tương ứng là tia phân giác của các góc tạo bởi AH và hai tiam Am, An của đường thẳng mn ?
Cho tam giác ABC có cạnh BC= 9.95 cm, góc ABC= 114°43'12", góc BCA= 20°46'48". Từ A vẽ các đường cao AH, đường phân giác trong AD, đường phân giác ngoài AE, và đường trung tuyến AM. Tính độ dài các cạnh còn lại của tam giác ABC và các đoạn thẳng AH, AD, AE, AM ( làm tròn kết quả đến hàng phần trăm )