Cho tứ giác ABCD >Chứng minh rằng :
AC+BD>AB+CD
Cho hình thang ABCD có AB // CD. Chứng minh rằng: Nếu AD+AC=BC+BD thì tứ giác ABCD là hình thang cân
Cho tứ giác ABCD có AB + BD \(_{^{ }\le}\) AC + CD. Chứng minh : AB < AC
Cho tứ giác ABCD có AB//CD và CD>AB. Gọi E, F lần lượt là trung điểm của BD và AC. Chứng minh rằng EF= (CD-AB)/2
Tứ giác ABCD có AB = BC, CD = DA. Chứng minh rằng BD là đường trung trực của AC.
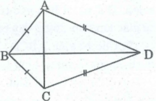
Ta có: BA = BC (gt). Suy ra điểm B thuộc đường trung trực của AC.
Lại có: DA = DC (gt). Suy ra điểm D thuộc đường trung trực của AC.
Vì B và D là 2 điểm phân biệt cùng thuộc đường trung trực của AC nên đường thẳng BD là đường trung trực của AC.
1. Cho hình thang ABCD có góc A = góc D = 90 độ , đáy nhỏ AB = a , cạnh bên BC = 2 a . Gọi M , N lần lượt là trung điểm AD , AB
a / Tính số đo các góc ABC , BAN
b/ Chứng minh tam giác NAD đều
c/ Tính MN theo a
2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C = 70 độ , góc D = 40 độ
b/ Cho hình thang ABCD có AB // CD và góc A = góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 = AB^2 + CD^2 + 2AD^2
3. Cho tứ giác ABCD :
a/ Chứng minh rằng AB + CD < AC + BD
b/ Cho biết AB + BD < hoặc = AC + CD
Chứng minh rằng AB < AC
4. Cho hình thang ABCD có AC vuông góc BD . CHứng minh rằng :
a/ AB^2 + CD^2 = AD^2 + BC^2
b/ ( AB + CD )^2 = AC^2 + BD^2
bạn hỏi thế này thì chả ai muốn làm -_- dài quá
Bạn gửi từng câu nhò thì các bạn khác dễ làm hơn!
dài quà làm sao mà có thòi gian mà trả lời .bạn hỏi ít thoi chứ
Cho tứ giác ABCD , gọi MN , PQ lần lượt là trung điểm AB , BC , CD , DA và AC = BD . Chứng minh rằng tứ giác MNPQ là hình thoi
bài này khá dễ , áp dụng đường trung bình trong tam giác , sau đó áp dụng giả thiết AC = BD
Cho tứ giác ABCD có AC=BD và AC vuông goác BD , Gọi M , N, Q lần lượt là trung điểm của các cạnh AB , BC , CD , DA . Chứng minh rằng tứ giác MNPQ là hình vuông
Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MNPQ là hình bình hành(5)
Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2=BD/2=MQ(3) và MN//AC
=>MN vuông góc với MQ(4)
Từ (3), (4)và (5) suy ra MNPQ là hình vuông
Cho tứ giác ABCD có AC=BD và AC vuông goác BD , Gọi M , N, Q lần lượt là trung điểm của các cạnh AB , BC , CD , DA . Chứng minh rằng tứ giác MNPQ là hình vuông
a: Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MNPQ là hình bình hành(5)
Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2=BD/2=MQ(3) và MN//AC
=>MN vuông góc với MQ(4)
Từ (3), (4)và (5) suy ra MNPQ là hình vuông
Cho tứ giác ABCD có AC=BD và AC vuông goác BD , Gọi M , N, Q lần lượt là trung điểm của các cạnh AB , BC , CD , DA . Chứng minh rằng tứ giác MNPQ là hình vuông
Trong tam giác ABD có: MQ là đường trung bình
=> MQ = 1/2 BD (1)
Trong tam giác ABC có : MN là đường trung bình
=> MN = 1/2 AC (2)
mà AC = BD và AC vuông góc với BD (3)
Từ (1) (2) và (3) => MQ = MN và MQ vuông góc với MN
=> tứ giác MNPQ là hình vuông