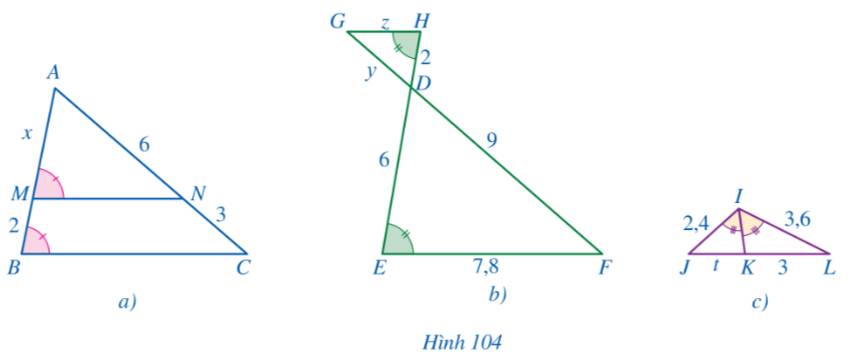
Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c.
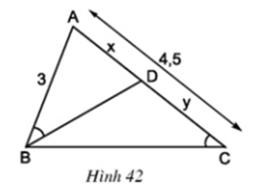
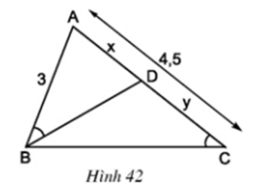
Ở hình 42 cho biết AB = 3cm; AC = 4,5cm và ∠(ABD) = ∠(BCA).
a) Trong hình vẽ này có bao nhiêu tam giác ? Có cặp tam giác nào đồng dạng với nhau không ?
b) Hãy tính các độ dài x và y (AD = x, DC = y).
c) Cho biết thêm BD là tia phân giác của góc B. Hãy tính độ dài các đoạn thẳng BC và BD.
a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC
ΔABD và ΔACB có
∠B = ∠C
∠A chung
⇒ ΔABD ∼ ΔACB (g.g)
b) Theo a ta có :
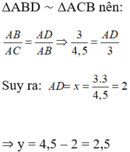
c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:
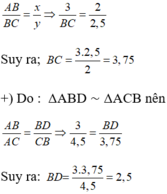
Ở hình 42 cho biết AB = 3cm; AC = 4,5cm và ∠(ABD) = ∠(BCA).
a) Trong hình vẽ này có bao nhiêu tam giác ? Có cặp tam giác nào đồng dạng với nhau không ?
b) Hãy tính các độ dài x và y (AD = x, DC = y).
c) Cho biết thêm BD là tia phân giác của góc B. Hãy tính độ dài các đoạn thẳng BC và BD.
a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC
ΔABD và ΔACB có
∠B = ∠C
∠A chung
⇒ ΔABD ∼ ΔACB (g.g)
b) Theo a ta có :
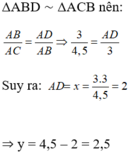
c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:
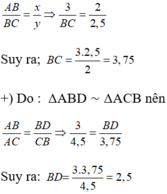
Kết quả thí nghiệm của các dung dịch X, Y, Z, T với thuốc thử ở nhiệt độ thường được ghi lại trong bảng sau.
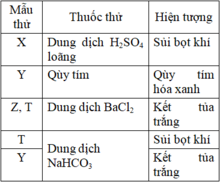
Các chất X, Y, Z, T lần lượt là
A. NaNO3, Na2CO3, CuSO4, H2SO4
B. FeCO3, Ca(OH)2, AgNO3, K2 SO4
C. Fe(NO3)2, Ca(OH)2, AgNO3, KHSO4
D. NaOH, Fe(NO3)2, KH SO4, H2SO4
Đáp án C.
(a) Đúng. Hỗn hợp CaF2 và H2SO4 đặc phản ứng với nhau ở điều kiện thích hợp tạo thành HF có khả năng ăn mòn thủy tinh.
(b)Đúng. Trong tự nhiên, không gặp photpho ở trạng thái tự do vì nó khá hoạt động về mặt hóa học. Hai khoáng vật chính của photpho là Apatic 3Ca3(PO4)2.CaF2 và Photphorit Ca3(PO4)2.
(c) Đúng. CrO3 và K2Cr2O7 đều có số oxi hóa cao nhất của Cr (+6) nên có tính oxi hóa mạnh (nhận e) để tạo thành các hợp chất ở mức oxi hóa thấp hơn.
(d) Sai. Nguyên tắc luyện gang là dùng than cốc khử quặng oxit sắt trong lò cao.
(e) Đúng.
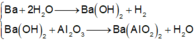
Chu vi của hình chữ nhật men là 104c của viên gạch.Tính độ dài một cạch cuả viên gạch đó .
độ dài 1 cạnh là:
104 : 4 = 86 (cm)
Độ dài một cạnh của viên gạch là : 104 : 4 = 86 ( cm )
Đáp số : 86 cm
Cho hình chóp S.ABC có độ dài các cạnh: S A = B C = x , S B = A C = y , S C = A B = z thỏa mãn x 2 + y 2 + z 2 = 12 . Tính giá trị lớn nhất của thể tích khối chóp S.ABC.
A. 2 3
B. 8 3
C. 2 2 3
Đáp án C
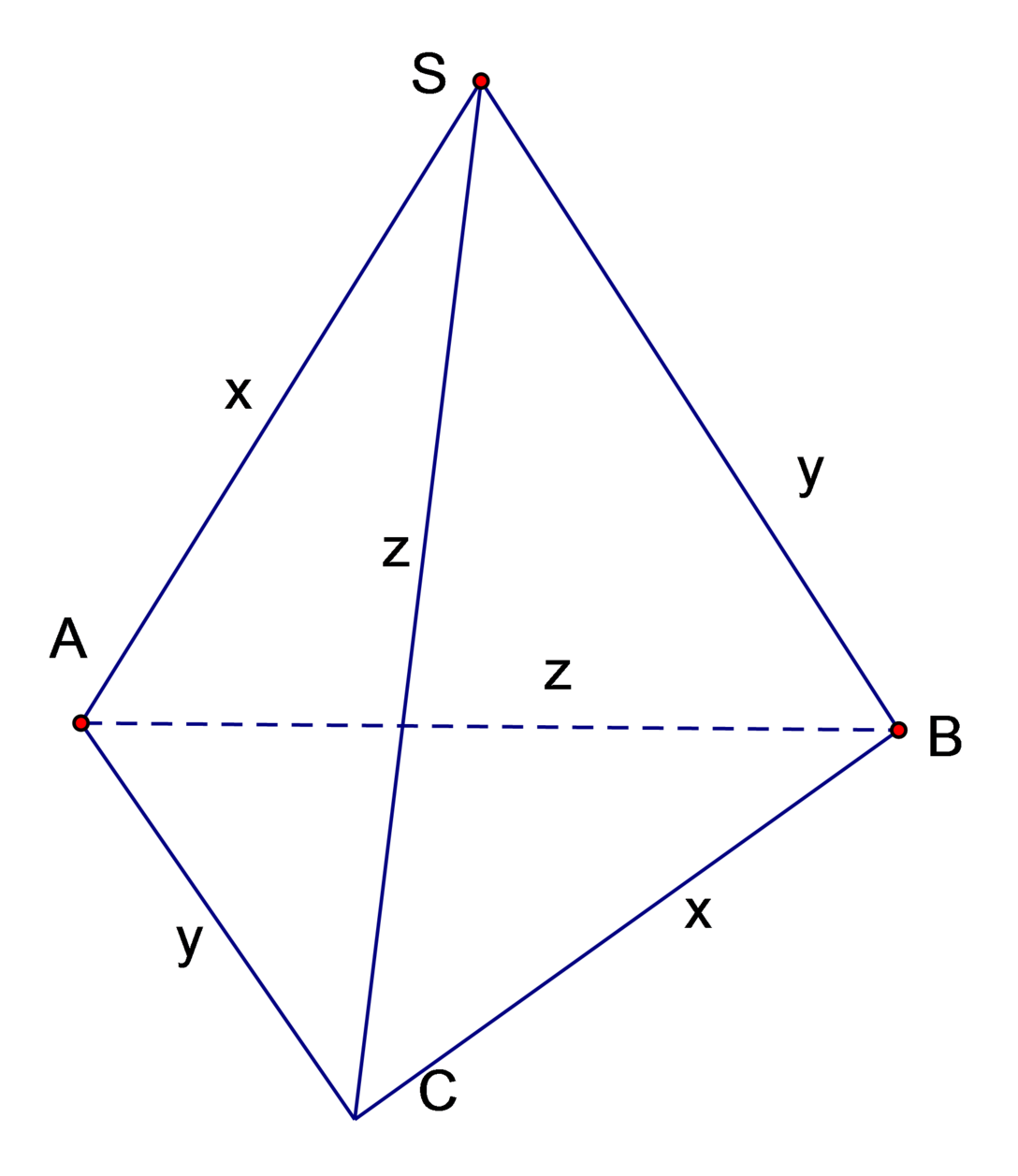
Áp dụng công thức tính thể tích tứ diện có hai cặp cạnh đối bằng nhau:
V S A B C = 1 6 2 x 2 + y 2 − z 2 y 2 + z 2 − x 2 z 2 + x 2 − y 2 ≤ 1 6 2 x 2 + y 2 − z 2 + y 2 + z 2 − x 2 + z 2 + x 2 − y 2 3 3 = 1 6 2 x 2 + y 2 + z 2 3 3 = 1 6 2 12 3 3 = 1 6 2 .8 = 2 2 3
Như vậy V S A B C lớn nhất bằng 2 2 3 khi: x=y=z=2
Tính độ dài x, y trong các hình bên
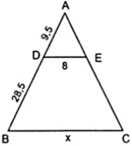
Áp dụng hệ quả của định lí Ta – lét ta có:
DE//BC ⇒ BC/DE = AB/AD hay x/8 = 28,5/9,5
⇔ x = (8.28,5)/9,5 = 456/19 ≈ 31,58
Tính độ dài x, y trong các hình bên
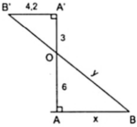
Ta có: A'B'//AB vì cùng vuông góc AA'
Áp dụng hệ quả của định lí Ta – lét ta có:
A'B'//AB ⇒ AB/A'B' = AO/A'O hay x/4,2 = 6/3 ⇔ x = 8,4
Áp dụng định lí Py – ta – go với Δ OAB ta có:
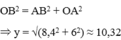
Tính độ dài x, y trong các hình bên
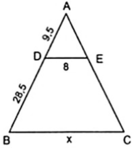
Áp dụng hệ quả của định lí Ta – lét ta có:
DE//BC ⇒ BC/DE = AB/AD hay x/8 = 28,5/9,5
⇔ x = 8.28,5/9,5 = 456/19 ≈ 31,58
Tính độ dài x, y trong các hình bên
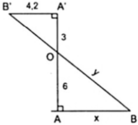
Ta có: A'B'//AB vì cùng vuông góc AA'
Áp dụng hệ quả của định lí Ta – lét ta có:
A'B'//AB ⇒ AB/A'B' = AO/A'O hay x/4,2 = 6/3 ⇔ x = 8,4
Áp dụng định lí Py – ta – go với Δ OAB ta có:
O B 2 = A B 2 + O A 2 ⇒ y = 8 , 4 2 + 6 2 ≈ 10 , 32