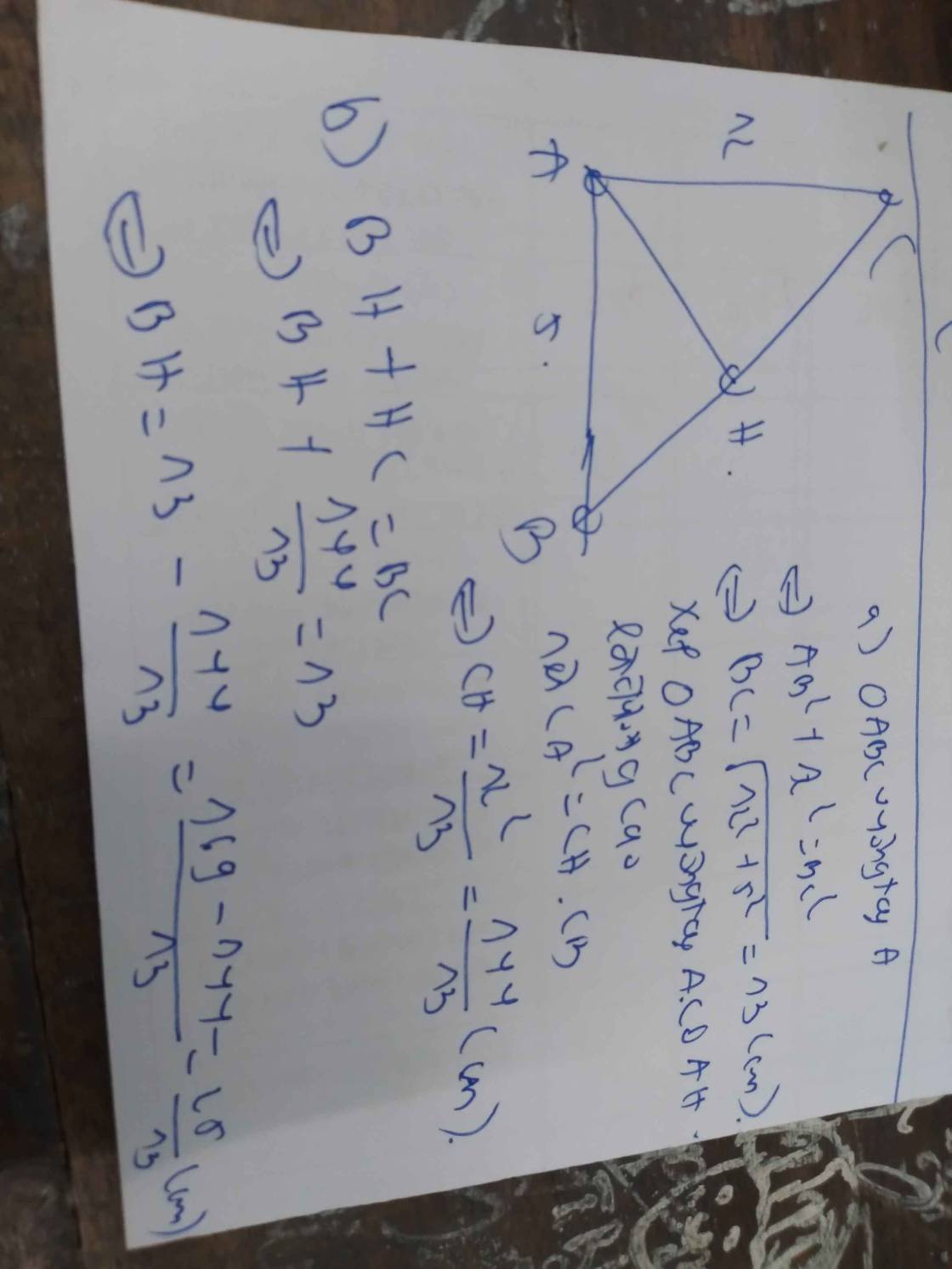
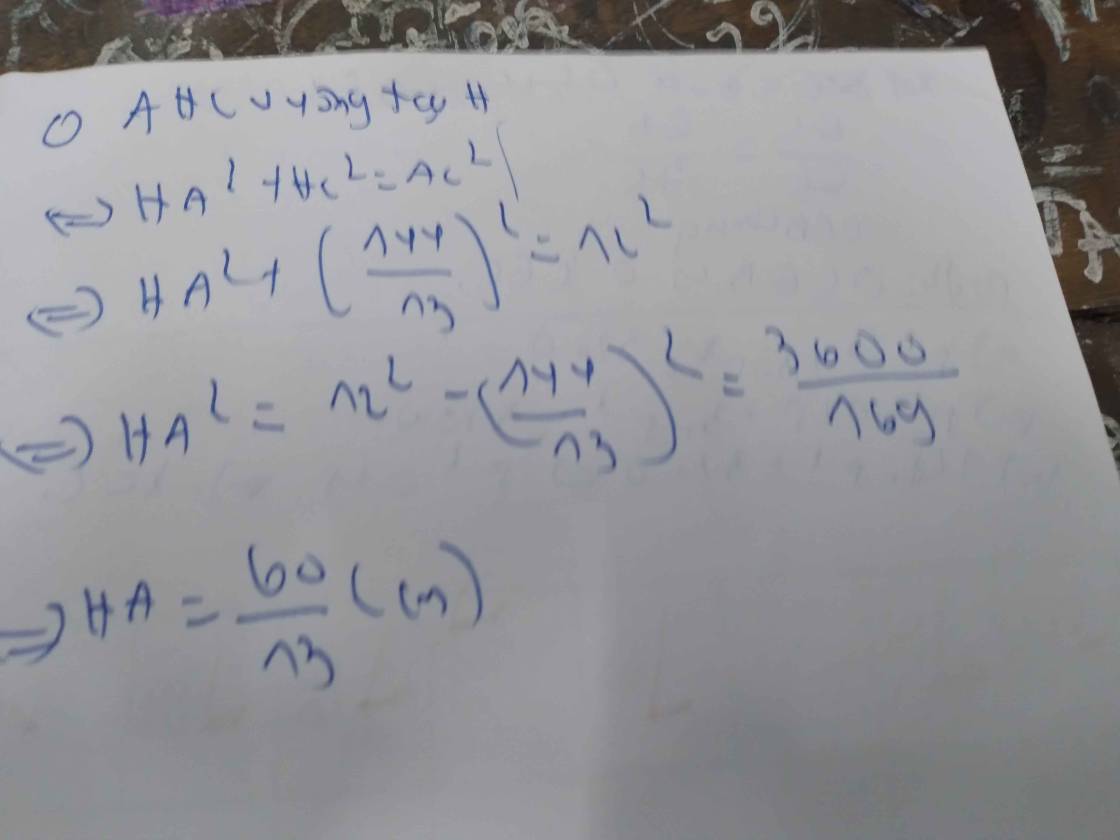tgiac ABC vuông tại A đường cao AH có AB =5cm BH=4cm tính AH CH AC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết BH = 4cm, CH = 5cm. Tính AB, AC
b) Biết AB = 10cm, AH = 6cm, tính BH, AC
a: BC=4+5=9(cm)
\(AB=\sqrt{4\cdot9}=6\left(cm\right)\)
\(AC=\sqrt{5\cdot9}=3\sqrt{5}\left(cm\right)\)
b: \(BH=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(CH=\dfrac{AH^2}{BH}=4,5\left(cm\right)\)
\(AC=\sqrt{6^2+4.5^2}=7,5\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH. Biết AB : AC = 3 : 4; AB + AC = 21
a) tính độ dài các cạnh tgiac ABC
b) tính AH,BH,CH
Hình tự vẽ
a) Ta có: AB : AC = 3 : 4
=> \(\frac{AB}{3}=\frac{AC}{4}=\frac{AB+AC}{3+4}=\frac{21}{7}=3\)
=> \(AB=9;\)\(AC=12\)
Áp dụng Pytago ta có:
BC2 =AB2 + AC2
<=> BC2 = 92 + 122 = 225
<=> BC = 25
b) Áp dụng hệ thức lượng ta có:
\(AH.BC=AB.AC\)
=> \(AH=\frac{AB.AC}{BC}=7,2\)
\(AB^2=BH.BC\)
=> \(BH=\frac{AB^2}{BC}=5,4\)
=> \(CH=BC-BH=9,6\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH. Biết AB : AC = 3 : 4; AB + AC = 21
a) tính độ dài các cạnh tgiac ABC
b) tính AH,BH,CH
Hình tự vẽ
a) Ta có: AB : AC = 3 : 4
=> \(\frac{AB}{3}=\frac{AC}{4}=\frac{AB+AC}{3+4}=\frac{21}{7}=3\)
=> \(AB=9;\)\(AC=12\)
Áp dụng Pytago ta có:
BC2 =AB2 + AC2
<=> BC2 = 92 + 122 = 225
<=> BC = 25
b) Áp dụng hệ thức lượng ta có:
\(AH.BC=AB.AC\)
=> \(AH=\frac{AB.AC}{BC}=7,2\)
\(AB^2=BH.BC\)
=> \(BH=\frac{AB^2}{BC}=5,4\)
=> \(CH=BC-BH=9,6\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH. Biết AB : AC = 3 : 4; AB + AC = 21
a) tính độ dài các cạnh tgiac ABC
b) tính AH,BH,CH
Hình tự vẽ
a) Ta có: AB : AC = 3 : 4
=> \(\frac{AB}{3}=\frac{AC}{4}=\frac{AB+AC}{3+4}=\frac{21}{7}=3\)
=> \(AB=9;\)\(AC=12\)
Áp dụng Pytago ta có:
BC2 =AB2 + AC2
<=> BC2 = 92 + 122 = 225
<=> BC = 25
b) Áp dụng hệ thức lượng ta có:
\(AH.BC=AB.AC\)
=> \(AH=\frac{AB.AC}{BC}=7,2\)
\(AB^2=BH.BC\)
=> \(BH=\frac{AB^2}{BC}=5,4\)
=> \(CH=BC-BH=9,6\)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại B, kẻ CH vuông góc AB. Biết AH= 1cm, BH= 4cm. Tính độ dài AC.
Bài 2: Cho tam giác ABC vuông tại A. Cạnh AB= 5cm đường cao AH, BH= 3cm, CH= 8cm. Tính AC.
Bài 3: Cho tam giác ABC vuông tại A, có \(\frac{AB}{BC}=\frac{3}{5}\)và AC= 16cm. Tính độ dài các cạnh AB=BC.
Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Đúng 0
Bình luận (0)
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC
Đúng 0
Bình luận (0)
1.Cho tam giác ABC vuông tại A. Gọi H là chân đường cao hạ từ A. Biết rằng AB = 7cm, AC = 9cm. Tính BH, CH, AH.
2. Cho tam giác ABC vuông tại A, đường cao AH. BH = 4cm, CH=9cm. Tính AH,AB,AC?
BÀI 2 : áp dụng hệ thức lượng trong tam giác, ta có: AH^2=BH*CH=>AH^2= 4*9=36=>AH=căn bậc hai của 36=6
\(AB^2=BH\cdot BC=4\cdot\left(4+9\right)=52=>AB=\sqrt{52}=2\sqrt{13}\)
\(AC^2=CH\cdot BC=9\cdot13=117=>AC=\sqrt{117}=3\sqrt{13}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB 3cm, BC 5cm. AH là đường cao. Tính BH, CH, AC và AH. A. BH 2cm, CH 3,2cm, AC 4cm, AH 2,4cm B. BH 1,8cm; CH 3,2cm; AC 4cm; AH 2,4cm C. BH 1,8cm; CH 3,2cm; AC 3cm; AH 2,4cm D. BH 1,8cm; CH 3,2cm; AC 4cm; AH 4,2cm
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.
A. BH = 2cm, CH = 3,2cm, AC = 4cm, AH = 2,4cm
B. BH = 1,8cm; CH = 3,2cm; AC = 4cm; AH = 2,4cm
C. BH = 1,8cm; CH = 3,2cm; AC = 3cm; AH = 2,4cm
D. BH = 1,8cm; CH = 3,2cm; AC = 4cm; AH = 4,2cm
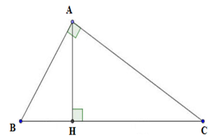
Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có:
![]()
+ Theo hệ thức lượng trong tam giác vuông ta có:
A B 2 = BH. BC => BH = A B 2 B C = 3 2 5 = 9 5 = 1 , 8 c m
Mà BH + CH = BC => CH = BC – BH = 5 – 1,8 = 3,2 cm
Lại có AH. BC = AB.AC => AH = A B . A C B C = 3.4 5 = 2,4cm
Vậy BH = 1,8cm, CH = 3,2cm, AC = 4cm, AH = 2,4 cm
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Cho tam giác ABC Vuông tại A có AH là đường cao. Biết AB=5cm AC= 12cm a) Tính BC,CH b) Tính AH,BH
Cho tam giác ABC vuông tại A có AB=3cm, BC=5cm. AH là đường cao. Tính cạnh BH, CH, AC và AH
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=16\)
hay AC=4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=1.8cm\\CH=3.2cm\\AH=2.4cm\end{matrix}\right.\)
Đúng 1
Bình luận (0)

Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có:
+ Theo hệ thức lượng trong tam giác vuông ta có:
A B 2 = BH. BC => BH = A B 2 B C = 3 2 5 = 9 5 = 1 , 8 c m
Mà BH + CH = BC => CH = BC – BH = 5 – 1,8 = 3,2 cm
Lại có AH. BC = AB.AC => AH = A B . A C B C = 3.4 5 = 2,4cm
Vậy BH = 1,8cm, CH = 3,2cm, AC = 4cm, AH = 2,4 cm
Đúng 0
Bình luận (0)