Tìm max
F= -5x^2 -4x +3
Tìm max
F= -5x^2 -4x +3
Lời giải:
$-F=5x^2+4x-3=5(x^2+\frac{4}{5}x+\frac{2^2}{5^2})-\frac{19}{5}$
$=5(x-\frac{2}{5})^2-\frac{19}{5}\geq \frac{-19}{5}$ với mọi $x$
$\Rightarrow F\leq \frac{19}{5}$
Vậy $F_{\max}=\frac{19}{5}$. Giá trị này đạt tại $x-\frac{2}{5}=0\Leftrightarrow x=\frac{2}{5}$
Tìm max
F= -5x^2 -4x +3
Tìm min
F=3x^2 +x -2
G= 4x^2+2x-1
H=5x^2-x+1
Tìm max
A= -x^2 -6x+3
B=-x^2+8x-1
C= -x^2-3X+4
D= -2x^2+3x-1
E= -3x^2 – x +2
F= -5x^2 -4x +3
G= -3x^2 – 5x+1
Tìm min:
$F=3x^2+x-2=3(x^2+\frac{x}{3})-2$
$=3[x^2+\frac{x}{3}+(\frac{1}{6})^2]-\frac{25}{12}$
$=3(x+\frac{1}{6})^2-\frac{25}{12}\geq \frac{-25}{12}$
Vậy $F_{\min}=\frac{-25}{12}$. Giá trị này đạt tại $x+\frac{1}{6}=0$
$\Leftrightarrow x=\frac{-1}{6}$
Tìm min
$G=4x^2+2x-1=(2x)^2+2.2x.\frac{1}{2}+(\frac{1}{2})^2-\frac{5}{4}$
$=(2x+\frac{1}{2})^2-\frac{5}{4}\geq 0-\frac{5}{4}=\frac{-5}{4}$ (do $(2x+\frac{1}{2})^2\geq 0$ với mọi $x$)
Vậy $G_{\min}=\frac{-5}{4}$. Giá trị này đạt tại $2x+\frac{1}{2}=0$
$\Leftrightarrow x=\frac{-1}{4}$
Tìm min
$H=5x^2-x+1=5(x^2-\frac{x}{5})+1$
$=5[x^2-\frac{x}{5}+(\frac{1}{10})^2]+\frac{19}{20}$
$=5(x-\frac{1}{10})^2+\frac{19}{20}\geq \frac{19}{20}$
Vậy $H_{\min}=\frac{19}{20}$. Giá trị này đạt tại $x-\frac{1}{10}=0$
$\Leftrightarrow x=\frac{1}{10}$
Tìm max -4xy+4x-y^2-5x^2+3
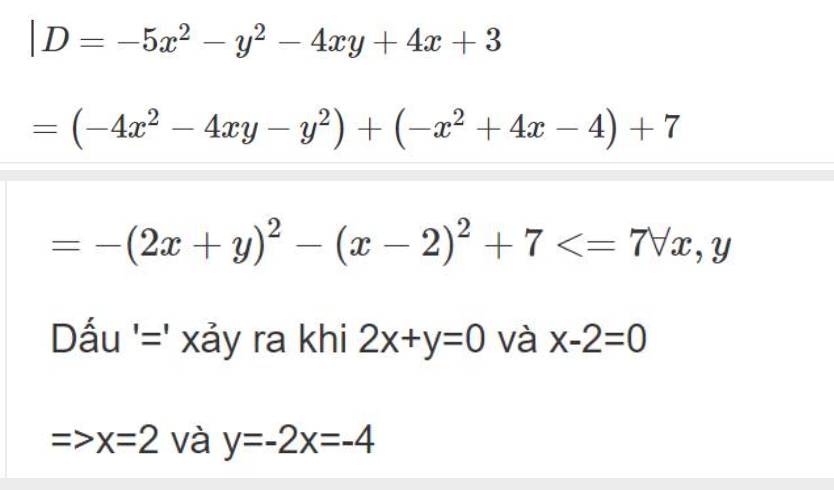
Vậy: \(D_{max}=7\) khi x=2 và y=-4
Tìm min:
A= x2 -6x-4
B= x2 -x+1
C= 5x2 +x-3
Tìm max:
D= -x2 +3x-1
E= -3x2 +4x+2
F= 6x - 7x2 -2
Tìm max hoặc min của A= -2x^2-8x+1
B=3x^2+3x-1
C=7x-2x^2+3
D=-4xy+4x-y^2-5x^2+3
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
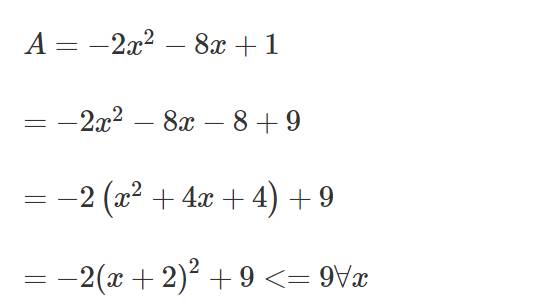
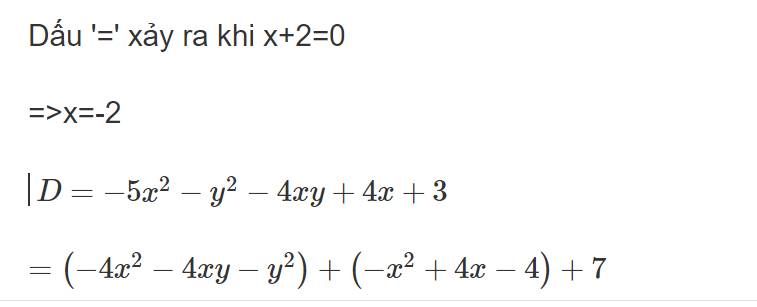
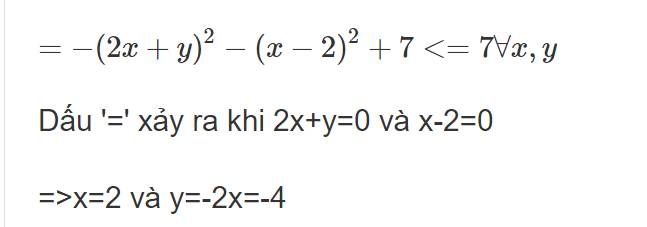
tìm Max A=(5x^2+4x-1)/x^2
1/Tìm Max B= 5-x2+2x-4y2-4
2/ Tìm x bít x3+5x2-4x-20=0
Tìm min:
A= x2 -6x-4
B= x2 -x+1
C= 5x2 +x-3
Tìm max:
D= -x2 +3x-1
E= -3x2 +4x+2
F= 6x - 7x2 -2
\(A=x^2-6x-4=x^2-6x+9-13=\left(x-3\right)^2-13\ge-13\)
Vậy \(A_{min}=-13\Leftrightarrow x=3\)
\(B=x^2-x+1=x^2-2.\frac{1}{2}x+\frac{1}{4}+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Vậy \(B_{min}=\frac{3}{4}\Leftrightarrow x=\frac{1}{2}\)
\(C=5x^2+x-3=5\left(x^2+\frac{1}{5}x-\frac{3}{5}\right)\)
\(=5\left(x^2+2.\frac{1}{10}x+\frac{1}{100}-\frac{61}{100}\right)\)
\(=5\left[\left(x+\frac{1}{10}\right)^2-\frac{61}{100}\right]=5\left(x+\frac{1}{10}\right)^2-\frac{61}{20}\ge\frac{-61}{20}\)
Vậy \(C_{min}=\frac{-61}{20}\Leftrightarrow x=\frac{-1}{10}\)