Cho tứ giác ABCD ngoại tiếp đường tròn I. Chứng minh AB + CD = AD + BC ( định lý Pithot thuận )

Những câu hỏi liên quan
Tứ giác ABCD có đường tròn (O) đường kính AB tiếp xúc CD. Chứng minh đường tròn (I) đường kính CD tiếp xúc AB <=>AD//BC.
Tứ giác ABCD nội tiếp đường tròn đường kính AD, có AB = BC = 4√3cm; CD = 4cm. Bán kính đường tròn ngoại tiếp tứ giác ABCD là ............ cm.
Lời giải:
Gọi giao của $BO$ và $AC$ là $H$
Vì $BA=BC; OA=OC$ nên $BO$ là trung trực của $AC$
$\Rightarrow BO$ vuông góc với $AC$ tại trung điểm $H$ của $AC$.
Do đó $HO$ là đường trung bình ứng với cạnh $CD$ của tam giác $ACD$
$\Rightarrow HO=2$
$BH=BO-HO=R-2$
Theo định lý Pitago:
$BC^2-BH^2=CH^2=CO^2-HO^2$
$\Leftrightarrow (4\sqrt{3})^2-(R-2)^2=R^2-2^2$
$\Leftrightarrow 48-(R-2)^2=R^2-4$
$\Rightarrow R=6$ (cm)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD nội tiếp đường tròn tâm O (AB>CD). GỌi giao điểm của AC và BD là I. Đường tròn ngoại tiếp tam giác ADI cắt AB và CD lần lượt tại E và F, EF cắt AC và BD tại M, N.
a, Chứng minh IE = IF
b, Chứng minh EF//BC và tứ giác AMND nội tiếp
c, Gọi K là tâm đường tròn ngoại tiếp tam giác ADI.
Chứng minh rằng KI vuông góc với BC
(Mình cần làm giúp phần (c) thôi ạ, cảm ơn)
Cho tứ giác ABCD nội tiếp đường tròn (O), AD cắt BC ở N. Gọi (O’) là đường tròn
ngoại tiếp tam giác NAB, (I) là đường tròn ngoại tiếp tam giác NCD. (O’) cắt (I) tại điểm thứ
hai K. Chứng minh O’I // OK.
cho tam giác ABC vuông tại A tren canh AC lấy điểm M đường tròn đường kính MC cắt BC tại E , BM cắt đườn tròn tại D chứng minh tứ giác ABCD nội tiếp xác định tâm I của đường tròn ngoại tiếp ? DB là phân giác góc ADE ? AB,ME,CD đồng quy tại một điểm?
cho tứ giác ABCD nội tiếp (o) có AD cắt BC tại E , AB cắt CD tại F . Gọi EI là đường đối trung của tam giác EAB ( I nằm trên đường tròn ngoại tiếp tam giác AEB) . FI cắt (o) lần lượt tại M , N . Chứng tỏ rằng IM = IN .
Gọi M là điểm bất kì thuộc đường tròn (O) ngoại tiếp tứ giác ABCD. Khoảng cách từ M đến đường thẳng AB, BC, CD, AD theo thứ tự là MH, MK, MI, MN. Chứng minh rằng MH.MI = MK.MN.
Cho tam giác ABC có
B
A
C
^
45
0
, các góc B và C đều nhọn. Đường tròn đường kính BC cắt AB và AC lần lượt tai D và E. Gọi H là giao điểm của CD và BEa, Chứng minh AE BEb, Chứng minh tứ giác ADHE nội tiếp. Xác định tâm K của đường tròn ngoại tiếp tứ giác nàyc, Chứng minh OE là tiếp...
Đọc tiếp
Cho tam giác ABC có B A C ^ = 45 0 , các góc B và C đều nhọn. Đường tròn đường kính BC cắt AB và AC lần lượt tai D và E. Gọi H là giao điểm của CD và BE
a, Chứng minh AE = BE
b, Chứng minh tứ giác ADHE nội tiếp. Xác định tâm K của đường tròn ngoại tiếp tứ giác này
c, Chứng minh OE là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE
d, Cho BC = 2a. Tính diện tích viên phân cung D E ⏜ của đường tròn (O) theo a
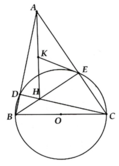
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm
Đúng 0
Bình luận (0)
Cho tứ giác ABCD nội tiếp đường tròn đồng thời lại ngoại tiếp một đường tròn khác có các tiếp điểm M,N,P,Q lần lượt với các cạnh AB , BC , CD , DA của tứ giác đã cho . Chứng minh rằng MP vuông góc với NQ












