1/Cho hình thang cân ABCD (AD//BC).Có góc B=2A.Tính góc C.
2/Cho hình thang cân ABCD (AB//CD).Gọi O là giao điểm của AC và BD.Biết rằng OA=2cm.OD=3cm.Tính độ dài đoạn thẳng AC.
1.Cho hình thang cân ABCD(AB//CD), góc BDC=45o. Gọi O là giao điểm của AC và BD.
a. CM tam giác DOC vuông cân
b. Tính diện tích của hình thang ABCD, biết BD=6cm
2. a. Tìm x của tứ giác ABCD, biết góc A=60 độ, góc C= 90 độ, góc D=63 độ
b. Cho hình thang ABCD(AB//CD). E,F lần lượt là trung điểm AD, BC. Tính độ dài đoạn thẳng EF, biết AB=3cm,CD=9cm
1) Cho hình thang cân ABCD (AB // CD). a) Chứng minh:. b) Gọi E là giao điểm của AC và BD. Chứng minh: . 2) Cho hình thang cân ABCD có đáy nhỏ CD = a , . Đường chéo AC vuông góc với cạnh bên BC. a) Tính các góc của hình thang. b) Chứng minh AC là phân giác của góc . c) Tính diện tích của hình thang.
Bài 1: Cho hình thang cân ABCD ( AB // CD) Gọi E là giao điểm của AC và BD. Chứng minh EA = EB.
Bài 2: Cho hình thang cân ABCD (AB//CD) có AB=3,BC=CD=13(cm). Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Tính độ dài BH.
Bài 3: Hình thang cân ABCD (AB//CD) có Cˆ=600, DB là tia phân giác của góc D, AB=4cm.
a) Chứng minh rằng BD vuông góc với BC.
b) Tính chu vi hình thang.
Bài 4 : Cho hình thang MNPQ (MN là đáy nhỏ) có 2 đường chéo MP và NQ cắt nhau tại O và NMPˆ=MNQˆA.
a) Chứng minh tam giác OMN và OPQ cân tại O.
b) Chứng minh tứ giác MNPQ là hình thang cân.
c) Qua O vẽ đường thẳng EF//QP (E∈MQ,F∈NP). Chứng minh MNFE, FEQP là những hình thang cân.
Bài 5: Cho hình thang cân ABCD (AB//CD, AB < CD). AD cắt BC tại O.
a) Chứng minh rằng ΔOAB cân.
b) Gọi I, J lần lượt là trung điểm của AB và CD. Chứng minh rằng ba điểm I, J, O thẳng hàng.
c) Qua điểm M thuộc cạnh AC, vẽ đường thẳng song song với CD, cắt BD tại N. Chứng minh rằng MNAB, MNDC là các hình thang cân.
Bài 1:
Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
Suy ra: \(\widehat{BAC}=\widehat{ABD}\)
hay \(\widehat{EAB}=\widehat{EBA}\)
hay ΔEAB cân tại E
Cho hình thang cân ABCD (AB//CD, AD = BC), có đáy nhỏ AB. Độ dài đường cao BH bằng độ dài đường trung bình MN (M thuộc AD, N thuộc BC) của hình thang ABCD. Vẽ BE//AC (E thuộc DC). Gọi O là giao điểm của AC và BD. Chứng minh rằng
a) MN = \(\frac{DE}{2}\)
b) Tam giác OAB cân
c) Tam giác DBE vuông cân
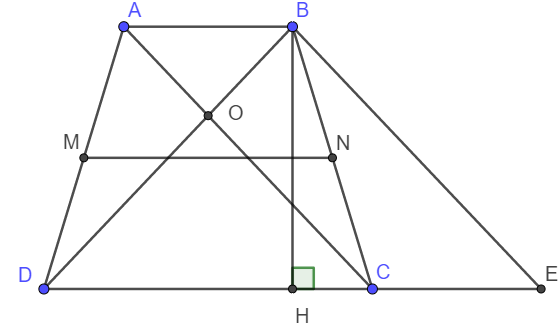
a) Xét tứ giác ABEC có AB // CE; AC // BE .
Vậy nên ABEC là hình bình hành. Suy ra AB = CE.
Do MN là đường trung bình hình thang ABCD nên ta có :
\(MN=\frac{AB+DC}{2}=\frac{CE+DC}{2}=\frac{DE}{2}.\)
b) Do ABCD là hình thang cân nên ta có:
\(AD=BC;DB=AC\)
Xét tam giác ABD và tam giác BAC có:
Cạnh AB chung
AD = BC
BD = AC
\(\Rightarrow\Delta ABD=\Delta BAC\left(c-c-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{BAC}\) hay \(\widehat{ABO}=\widehat{BAO}\)
Xét tam giác OAB có \(\widehat{ABO}=\widehat{BAO}\) nê OAB là tam giác cân tại O.
c) Do ABEC là hình bình hành nên AC = BE
Lại có AC = BD nên BD = BE
Suy ra tam giác BDE cân tại B.
Tam giác cân BDE có BH là đường cao nên đồng thời là đường trung tuyến.
Lại có theo câu a thì MN = DE/2
Giả thiết lại cho MN = BH. Vậy nên BH = DE/2
Xét tam giác BDE có trung tuyến BH bằng một nửa cạnh tướng ứng nên BDE là tam giác vuông tại B.
Vậy BDE là tam giác vuông cân tại B.
Cho hình thang cân ABCD(AB//CD), AB=BC và BC vuông góc với BD
a) Chứng minh AC vuông góc với AD
b) Tính số đo các góc hình thang
c) Gọi O là giao điểm của 2 đường chéo. Chứng minh rằng O cách đều 2 cnhj bên và đáy lớn
d) Gọi M là giao điểm cảu AD và Bc. H là hình chiếu của O trên DC. Chứng minh M,H,O thẳng hàng
1,cho hình thang abcd (ab//cd) ac cắt bd tại o. biết oa=ob.chứng minh abcd là hình thang cân
2. cho hình thang cân abcd (ab//cd,ab<cd ). Ad cắt bc tại o
a > CMR Tam giac OAB cân
b > Gọi I,J lần lượt là trung điểm của Ab và Cd. CMR ba điểm I, J,O thẳng hàn
c, Qua diểm M thuộc cạnh Ac vẽ đường thằng // với cd,cắt bd tại N. CMR MNAB ,MNDC là các hình thang cân
vì oa=ob
=>tam giác aob là tam giác cân tại o (đn tam giác cân)
=>góc oab=góc oba
mà ab//cd
=> abcd là hình thang cân
đúng thì k cho mik vs ạ
Cho tứ giác ABCD gọi O là giao điểm của AC và BD.Biết rằng OA=OB,OC=OD.Chứng minh rằng tứ giác ABCD là hình thang cân.
Cho hình thang cân ABCD (AB//CD) và AD cắt BC tại E. Gọi O là giao điểm của AC và BD . C/m EO vuông góc AB và EO vuông góc với CD
a)
\(\Delta ABC\)vuông tại A
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=20\left(cm\right)\)
BD là đường phân giác của \(\Delta ABC\)
\(\Rightarrow\frac{AD}{AB}=\frac{CD}{BC}=\frac{AD+CD}{AB+BC}=\frac{AC}{AB+BC}=\frac{20}{15+25}=\frac{1}{2}\)
\(\Leftrightarrow\frac{AD}{AB}=\frac{1}{2}\Rightarrow AD=\frac{AB}{2}=\frac{15}{2}=7,5\left(cm\right)\)
b)
Xét \(\Delta ABC\)và \(\Delta HBA\)CÓ:
\(\widehat{BAC}=\widehat{AHB}\left(=90^ô\right)\)
\(\widehat{ABC}\)là góc chung (gt)
Suy ra \(\Delta ABC\)đồng dạng với \(\Delta HBA\)(g.g)
\(\Rightarrow\frac{AB}{HB}=\frac{BC}{BA}=\frac{AC}{AH}\Rightarrow\hept{\begin{cases}AH=\frac{AB.AC}{BC}\\HB=\frac{AB^2}{BC}\end{cases}\Leftrightarrow\hept{\begin{cases}AH=\frac{15.20}{25}=12\left(cm\right)\\HB=\frac{15^2}{25}=9\left(cm\right)\end{cases}}}\)
c)
Xét \(\Delta ABD\)và \(\Delta HBI\)có;
\(\widehat{BAD}=\widehat{BHI}=90^o\)
\(\widehat{ABD}=\widehat{HBI}\left(gt\right)\)
SUY RA \(\Delta ABD\)đồng dạng với \(\Delta HBI\)(g.g)
\(\Rightarrow\frac{AB}{HB}=\frac{BD}{BI}\Leftrightarrow AB.BI=BD=HB\)
d)
\(\Delta ABD\)đồng dạng với \(\Delta HBI\) ( Theo câu c)
\(\frac{AD}{HI}=\frac{AB}{HB}\Rightarrow HI=\frac{AD.HB}{AB}=\frac{7,5.9}{15}=4,5\left(cm\right)\)
Ta có:
\(AI=AH-HI=12-4,5=7,5\left(cm\right)\)
Mà AD=7,5 cm
nên \(\Delta ADI\)cân tại A
e)
\(\Delta ABD\)đồng dạng vớI \(\Delta HBI\)( Theo câu c)
\(\Rightarrow\frac{AD}{IH}=\frac{BD}{BI}\Leftrightarrow AI.BI=BD.IH\)
Cho hình thang cân ABCD AB CD, AD BC , có đáy nhỏ AB. Độ dài đường cao BH bằng độ dài đường trung bình MN M thuộc AD, N thuộc BC của hình thang ABCD. Vẽ BE AC E thuộc DC . Gọi O là giao điểm của AC và BD. Chứng minh rằnga MN DE2 b Tam giác DBE vuông cân