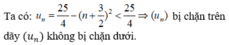Xét tính đơn điệu (Un) với Un=4n+3/3n+4

Những câu hỏi liên quan
Xét tính đơn điệu của dãy số sau:
a) un=\(\dfrac{\sqrt{n+1}-n}{n}\)
Cho dãy số u n v ớ i u n = 4 n - 2 ( n ≥ 1 ) . Xét tính tăng hay giảm của hàm số.
A. Dãy (un) tăng
B. Dãy (un) tăng
C. Dãy (un) không tăng, không giảm
D. Dãy (un) không đổi
Cho dãy số
(
u
n
)
với
u
n
1
+
2
+
3
+
4
+
.
.
.
+
n
(
1
+
3...
Đọc tiếp
Cho dãy số ( u n ) với u n = 1 + 2 + 3 + 4 + . . . + n ( 1 + 3 + 3 2 + 3 3 + . . . + 3 n ) . n + 1 . Tính l i m u n
A. 0
B. 2
C. 1 3
D. 1
* Xét tử số: Ta thấy 1, 2, 3, 4, ..., n là một dãy số thuộc cấp số cộng có n số hạng với
u 1 = 1 ; d= 1 .
Tổng n số hạng của cấp số cộng: S n = u 1 + u n n 2 = 1 + n n 2 .
* Xét mẫu số: Ta thấy 1 , 3 , 3 2 , 3 3 , ... , 3 n là một dãy số thuộc cấp số nhân có n + 1 số hạng với u 1 = 1 ; q = 3
Tổng (n+ 1) số hạng của cấp số nhân: S n + 1 = u 1 . 1 − q n + 1 1 − q = 1 − 3 n + 1 1 − 3 = 3 n + 1 − 1 2 .
⇒ u n = n 3 n + 1 − 1 = n 3.3 n − 1
Bằng quy nạp ta luôn có n < 2 n , ∀ n ∈ ℕ * và 3 n > 1 , ∀ n ∈ ℕ *
⇒ u n = n 3.3 n − 1 < n 3 n < 2 n 3 n = 2 3 n
Vì lim 2 3 n = 0 nên lim u n = 0.
Chọn đáp án A
Đúng 0
Bình luận (0)
Xét tính tăng, giảm của dãy số (un) có số hạng tổng quát un = 2n - 3n
Ta sẽ chứng minh dãy này giảm theo quy nạp.
Với n = 1 ta có u1 = -1
Với n = 2 ta có u2 = -5
=> u1 > u2
Giả sử dãy trên đúng với uk > uk+1 tức 2k - 3k > 2(k + 1) - 3k + 1 <=> 2k - 2(k + 1) > 3k - 3k+1
Ta cần chứng minh dãy cũng đúng với uk+1 > uk+2
Hay 2(k + 1) - 3k+1 > 2(k + 2) - 3k+2
<=> 2k - 3.3k > 2(k + 1) - 3.3k+1
<=> 2k - 2(k + 1) > 3.(3k - 3k+1)
Thật vậy: Với k nguyên dương ta luôn có 3k - 3k+1 < 0 và 3 > 1 nên 3(3k - 3k+1) < 3k - 3k+1
Lại có 2k - 2(k + 1) > 3k - 3k+1 => 2k - 2(k + 1) > 3.(3k - 3k+1) (đpcm)
Vậy dãy un trên là dãy giảm
Đúng 0
Bình luận (0)
Xét tính tăng, giảm và bị chặn của dãy số (un), biết:
u
n
n
2
+
3
n
+
1
n
+
1
A. Dãy số tăng, bị chặn trên B. Dãy số tăng, bị chặn dưới C. Dãy số giảm, bị chặn trên D. Cả A, B, C đều sai
Đọc tiếp
Xét tính tăng, giảm và bị chặn của dãy số (un), biết: u n = n 2 + 3 n + 1 n + 1
A. Dãy số tăng, bị chặn trên
B. Dãy số tăng, bị chặn dưới
C. Dãy số giảm, bị chặn trên
D. Cả A, B, C đều sai
Chọn B.
Ta có:
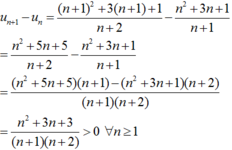
⇒ un+1 > un ∀ n ≥ 1 ⇒ dãy (un) là dãy số tăng.
un > 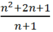 = n + 1 ≥ 2 ⇒ dãy (un) bị chặn dưới.
= n + 1 ≥ 2 ⇒ dãy (un) bị chặn dưới.
Đúng 0
Bình luận (0)
Xét tính bị chặn của các dãy số sau:
u
n
4
-
3
n
-
n
2
A. Bị chặn B. Không bị chặn C. Bị chặn trên D. Bị chặn dưới
Đọc tiếp
Xét tính bị chặn của các dãy số sau: u n = 4 - 3 n - n 2
A. Bị chặn
B. Không bị chặn
C. Bị chặn trên
D. Bị chặn dưới
Cho dãy số
(
u
n
)
với
u
n
-
5
n
+
4
n
-
7
n
+...
Đọc tiếp
Cho dãy số ( u n ) với u n = - 5 n + 4 n - 7 n + 1 + 4 n + 1 . Tính l i m u n
A. - 1 7
B. + ∞
C. 1 4
D. 0
Ta có: u n = − 5 n 1 + 4 n − 5 n − 7 n − 7 + 4.4 n − 7 n = 5 7 n ⋅ 1 + − 4 5 n − 7 + 4. − 4 7 n
Vì lim − 4 5 n = lim − 4 7 n = 0 nên lim 1 + − 4 5 n − 7 + 4. − 4 7 n = − 1 7 và lim 5 7 n = 0
Do đó lim u n = 0
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho dãy số
u
n
với
u
n
3
n
.
Tính
u
n
+
1
?
A.
u
n
+
1
3.3
n
B.
u...
Đọc tiếp
Cho dãy số u n với u n = 3 n . Tính u n + 1 ?
A. u n + 1 = 3.3 n
B. u n + 1 = 3 n + 1
C. u n + 1 = 3 n + 3
D. u n + 1 = 3 n + 1
Cho dãy số
(
u
n
)
với
u
n
4
n
2
+
1
-
2
n
n
2
+
4
n...
Đọc tiếp
Cho dãy số ( u n ) với u n = 4 n 2 + 1 - 2 n n 2 + 4 n + 1 - n . Tính l i m u n
A. + ∞
B. 2
C. 0
D. 1
Xét tử số : 4 n 2 + 1 − 2 n = 4 n 2 + 1 − 4 n 2 4 n 2 + 1 + 2 n = 1 4 n 2 + 1 + 2 n
Xét mẫu số: 1 n 2 + 4 n + 1 − n = n 2 + 4 n + 1 + n n 2 + 4 n + 1 − n 2 = n 2 + 4 n + 1 + n 4 n + 1
⇒ l i m u n = lim n 2 + 4 n + 1 + n 4 n 2 + 1 + 2 n 2 n + 1 = lim n 2 1 + 4 n + 1 n 2 + n n 2 4 + 1 n 2 + 2 n 2 n + 1 = lim n 1 + 4 n + 1 n 2 + 1 n 4 + 1 n 2 + 2 n 2 + 1 n = lim 1 + 4 n + 1 n 2 + 1 n 4 + 1 n 2 + 2 2 + 1 n = lim 2 n 2 + 2 2 = lim 1 4 n = 0.
Do đó lim u n = 0
Chọn đáp án C
Đúng 0
Bình luận (0)