chứng tỏ rằng từ tỉ lệ thức a/b=c/d suy ra tỉ lệ thức a^2/c^2=ab/cd

Những câu hỏi liên quan
Chứng tỏ rằng từ tỉ lệ thức a/b = c/d ta suy ra tỉ lệ thức
\(\frac{a.b}{c.d}=\frac{a^2+b^2}{c^2+d^2}\)
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{b}.\frac{c}{d}=\frac{a}{b}.\frac{a}{b}=\frac{a^2}{b^2};\frac{a}{b}.\frac{c}{d}=\frac{c}{d}.\frac{c}{d}=\frac{c^2}{d^2}\\ \Rightarrow\frac{a}{b}.\frac{c}{d}=\frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}\)
Đúng 0
Bình luận (3)
Chứng minh rằng từ tỉ lệ thức ab=cd(a−b≠0,c−d≠0)ab=cd(a−b≠0,c−d≠0) ta có thể suy ra tỉ lệ thức a+ba−b=c+dc−da+ba−b=c+dc−d
Chứng minh rằng từ tỉ lệ thức \(\frac{a}{b}=\frac{c}{d}\), ta có thể suy ra tỉ lệ thức \(\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}và\frac{ac}{bd}=\frac{a^2-c^2}{b^2-d^2}\)
Giả sử tất cả các tỷ lệ thức đều có nghĩa.
Từ: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
\(\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2-b^2}{c^2-d^2}=\frac{a}{c}\cdot\frac{a}{c}=\frac{a}{c}\cdot\frac{b}{d}=\frac{ab}{cd}\)
Tương tự từ tỷ lệ thức ban đầu \(\frac{a}{b}=\frac{c}{d}\)cũng suy ra: \(\frac{ac}{bd}=\frac{a^2-c^2}{b^2-d^2}\)
Đúng 0
Bình luận (0)
Chứng minh tỉ lệ thức \(\frac{a^2+b^2}{c^2+d^2}=\frac{ab}{cd}\)có thể suy ra tỉ lệ thức a/b = c/d
\(\frac{a^2+b^2}{c^2+d^2}=\frac{ab}{cd}\Leftrightarrow cd.\left(a^2+b^2\right)=ab.\left(c^2+d^2\right)\)
\(\Leftrightarrow cda^2+cdb^2=abc^2+abd^2\)
\(\Leftrightarrow cdb^2-abc^2=abd^2-cda^2\)
\(\Leftrightarrow cb.\left(db-ac\right)=ad.\left(bd-ca\right)\Leftrightarrow cb=ad\Leftrightarrow\frac{a}{b}=\frac{c}{d}\)(ĐK: bd-ac khác 0)
Đúng 0
Bình luận (0)
Cho a, b, c, d ≠ 0. Từ tỉ lệ thức a b = c d Hãy suy ra tỉ lệ thức: a - b a = c - d c
Vì a, b, c, d ≠ 0 nên ta có thể đặt 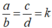 ⇒ a = kb; c = kd
⇒ a = kb; c = kd
Ta có:
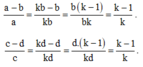
Suy ra 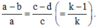
Cách 2:
Từ 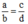 ta suy ra
ta suy ra 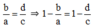 hay
hay 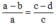
Đúng 0
Bình luận (0)
Chứng minh rằng từ tỉ lệ thức \(\frac{a}{b}=\frac{c}{d}\)ta suy ra được tỉ lệ thức \(\left(\frac{a+b}{c+d}\right)^2=\frac{a^2+b^2}{c^2+d^2}và\left(\frac{a+b}{c+d}\right)^2=\frac{ab}{cd}\)
Giả sử tất cả các tỷ lệ thức đều có nghĩa.
Từ: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)
Và suy ra: \(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{\left(a+b\right)^2}{\left(c+d\right)^2}=\frac{a^2+b^2}{c^2+d^2}\)
Và Từ: \(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\Rightarrow\frac{\left(a+b\right)^2}{\left(c+d\right)^2}=\frac{a}{c}\cdot\frac{b}{d}=\frac{ab}{cd}\)
Đúng 0
Bình luận (0)
Chứng minh tỉ lệ thức
a
b
c
d
(a - b ≠ 0, c - d ≠ 0) ta có thể suy ra tỉ lệ thức
a
+
b
a
-
b
c
+
d
c...
Đọc tiếp
Chứng minh tỉ lệ thức a b = c d (a - b ≠ 0, c - d ≠ 0) ta có thể suy ra tỉ lệ thức a + b a - b = c + d c - d
C/m rằng từ tỉ lệ thức a/b=c/d ta suy ra đc
ab/cd=(a-b)^2/(c-d)^2
Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk$. Khi đó:
$\frac{ab}{cd}=\frac{bk.b}{dk.d}=\frac{b^2}{d^2}(1)$
Và:
$\frac{(a-b)^2}{(c-d)^2}=\frac{(bk-b)^2}{(dk-d)^2}=\frac{b^2(k-1)^2}{d^2(k-1)^2}=\frac{b^2}{d^2}(2)$
Từ $(1); (2)$ ta có đpcm.
Đúng 0
Bình luận (0)
Chứng minh rằng từ tỉ lệ thức ab =cd (a−b≠0,c−d≠0) ta có thể suy ra tỉ lệ thức a+ba−b =c+dc−d .














