Tính tổng: 13+23+33+...+n3

Những câu hỏi liên quan
Chứng minh các đẳng thức sau (
v
ớ
i
n
∈
N
*
)
1
3
+
2
3
+
3
3
+
.
.
.
+
n
3...
Đọc tiếp
Chứng minh các đẳng thức sau ( v ớ i n ∈ N * ) 1 3 + 2 3 + 3 3 + . . . + n 3 = n 2 n + 1 2 4
Đặt vế trái bằng A n
Dễ thấy với n = 1 hệ thức đúng.
Giả sử đã có 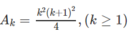
Ta có:
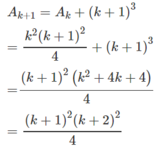
Đúng 0
Bình luận (0)
viết các tổng sau thành một bình phương a 13 23 33 43 53b 13 23 33 43 53 63
Viết các tổng sau thành một bình phương của một Số tự nhiên:a)
2
+
3
3
+
4
2
+
13
2
b)
1
3
+...
Đọc tiếp
Viết các tổng sau thành một bình phương của một Số tự nhiên:
a) 2 + 3 3 + 4 2 + 13 2
b) 1 3 + 2 3 + 3 3 + 4 3 + 5 3 + 6 3
a) 2 + 3 3 + 4 2 + 13 2 = 196 = 14 2
b, 1 3 + 2 3 + 3 3 + 4 3 + 5 3 + 6 3 = 441 = 21 2
Đúng 0
Bình luận (0)
Biết: 13+23+33+....+103=3025. Tính S= 23+43+63+...+203
huỳnh thị ngân hà, nau te, trần như tính sao ra z?
Đúng 0
Bình luận (0)
S = 13+10+23+20+33+30+...+103+100
S = 13+23+33+...+103+10.100
S = 3025+1000
S = 4025
Đúng 0
Bình luận (0)
6020 , chắc chắn đúng 10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000%
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tính hợp lí
\(\frac{\frac{6}{13}-\frac{6}{23}+\frac{6}{33}-\frac{6}{43}}{\frac{5}{13}-\frac{5}{23}+\frac{5}{33}-\frac{5}{43}}\)
\(\frac{\frac{6}{13}-\frac{6}{23}+\frac{6}{33}-\frac{6}{43}}{\frac{5}{13}-\frac{5}{23}+\frac{5}{33}-\frac{5}{43}}\)
= \(\frac{6.\left(\frac{1}{13}-\frac{1}{23}+\frac{1}{33}-\frac{1}{43}\right)}{5.\left(\frac{1}{13}-\frac{1}{23}+\frac{1}{33}-\frac{1}{43}\right)}\)
= \(\frac{6}{5}\)
k cho mình nhé
Đúng 0
Bình luận (0)
Bài 2: Các số sau có phải là số chính phương không?
1. 13 + 23 ; 13 + 23 + 33 ; 13 + 23 + 33 + 43 ; 13 + 23 + 33 + 43 + 53
2. 1262 + 1 ; 100! + 8 ; 1012 - 3 ; 1010 + 7 ; 11 + 112 + 113
3. 32 + 22 b) 62 + 82 c) 400 - 162 d) 2.3.45.7.9.11.13 + 2018 e) 13 + 23
4. m) 1262 + 1 n) 100!+ 8 p) 1012 - 3 q) 1010 + 7 k) 11 + 112 + 113
Mọi người trình bày đầy đủ hộ mình ạ!
Nhanh giúp ạ
Đọc tiếp
Bài 2: Các số sau có phải là số chính phương không?
1. 13 + 23 ; 13 + 23 + 33 ; 13 + 23 + 33 + 43 ; 13 + 23 + 33 + 43 + 53
2. 1262 + 1 ; 100! + 8 ; 1012 - 3 ; 1010 + 7 ; 11 + 112 + 113
3. 32 + 22 b) 62 + 82 c) 400 - 162 d) 2.3.45.7.9.11.13 + 2018 e) 13 + 23
4. m) 1262 + 1 n) 100!+ 8 p) 1012 - 3 q) 1010 + 7 k) 11 + 112 + 113
Mọi người trình bày đầy đủ hộ mình ạ!
Nhanh giúp ạ
Bài 1:
13 + 23 = 1 + 8 = 9 = 32 (là một số chính phương)
13 + 23 + 33 = 1 + 8 + 27 = 36 = 62 (là một số chính phương)
13 + 23 + 33 + 43 = 1 + 8 + 27 + 64 = 100 = 102 (là số cp)
13 + 23 + 33 + 43 + 53 = 1 + 8 + 27 + 64 + 125 = 225 = (15)2 là số cp
Đúng 1
Bình luận (0)
Bài 2:
1262 + 1 = \(\overline{..6}\) + 1 = \(\overline{...7}\) (không phải số chính phương)
100! + 8 = \(\overline{...0}\) + 8 = \(\overline{...8}\) (không phải là số chính phương)
1012 - 3 \(\overline{..01}\) - 3 = \(\overline{...8}\) (không phải là số chính phương)
107 + 7 = \(\overline{..0}\) + 7 = \(\overline{..7}\) (không phải là số chính phương)
11 + 112 + 113 = \(\overline{..1}\)+ \(\overline{..1}\)+ \(\overline{..1}\) = \(\overline{...3}\) (không phải số chính phương)
Đúng 1
Bình luận (0)
Bài 3:
32 + 22 = 9 + 4 = 13 (không phải là số chính phương)
62 + 82 = 36 + 64 = 100 = 102 (là số chính phương)
2.3.45.7.9.11.13 + 2018 = \(\overline{...0}\) + 2018 = \(\overline{..8}\) (không phải là số cp)
Bài 4 giống bài 2
Đúng 0
Bình luận (0)
(13/2020+23/2021-33/2022)-(1/2-1/3-1/6) tính nhanh
7/3*13+ 7/13*23+ 7/23*33+ 7/33*43+ 7/43*53+ 7/53*63
\(A=\frac{7}{3\times13}+\frac{7}{13\times23}+...+\frac{7}{53\times63}\)
\(A=\frac{7}{10}.\left[\left(\frac{1}{3}-\frac{1}{13}\right)+\left(\frac{1}{13}-\frac{1}{23}\right)+....+\left(\frac{1}{53}-\frac{1}{63}\right)\right]\)
\(A=\frac{7}{10}.\left(\frac{1}{3}-\frac{1}{13}+\frac{1}{13}-\frac{1}{23}+....+\frac{1}{53}-\frac{1}{63}\right)\)
\(A=\frac{7}{10}.\left(\frac{1}{3}-\frac{1}{63}\right)\)
\(A=\frac{7}{10}.\frac{20}{63}\)
\(A=\frac{2}{9}\)
Chứng minh:
1
3
+
2
3
1
+
2
Viết tiếp một số đẳng thức tương tự.
1
3
+
2
3...
Đọc tiếp
Chứng minh: 1 3 + 2 3 = 1 + 2
Viết tiếp một số đẳng thức tương tự.
1 3 + 2 3 + 3 3 = 1 + 2 + 3 1 3 + 2 3 + 3 3 + 4 3 = 1 + 2 + 3 + 4