Đặt vế trái bằng A n
Dễ thấy với n = 1 hệ thức đúng.
Giả sử đã có 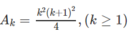
Ta có:
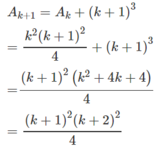
Đặt vế trái bằng A n
Dễ thấy với n = 1 hệ thức đúng.
Giả sử đã có 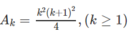
Ta có:
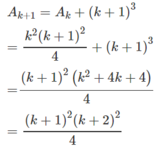
Chứng minh các đẳng thức sau (với n∈N∗n∈N∗)
a) 2+5+8+...+(3n−1)=n(3n+1)22+5+8+...+(3n−1)=n(3n+1)2;
b) 3+9+27+...+3n=12(3n+1−3)3+9+27+...+3n=12(3n+1−3).
Chứng minh các đẳng thức sau với n ∈ N ∗ B n = 1 + 3 + 6 + 10 + . . . + n n + 1 2 = n n + 1 n + 2 6
Chứng minh các bất đẳng thức sau 3n − 1 > n(n + 2) với n ≥ 4
Chứng minh rằng với mọi số tự nhiên n ≥ 2 , ta có các bất đẳng thức: 2 n + 1 > 2 n + 3
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) 2 n + 2 > 2 n + 5
Chứng minh đẳng thức sau ( v ớ i n ∈ N ∗ ) 2 + 5 + 8 + . . . + ( 3 n - 1 ) = 3 3 n + 1 2
Chứng minh các đẳng thức sau với n ∈ N ∗ A n = 1 1 . 2 . 3 + 1 2 . 3 . 4 + . . . + 1 n n + 1 n + 2 = n n + 3 4 n + 1 n + 2
Chứng minh các bất đẳng thức sau ( n ∈ N ∗ ) sin 2 n α + cos 2 n α ≤ 1 .
Help
Chứng minh rằng với mọi số nguyên n≥2n≥2, ta luôn có đẳng thức sau :
(1−14)(1−19)...(1−1n2)=n+12n
1) Gọi \(d\) là tổng độ dài các đường chéo của một đa giác lồi trong mặt phẳng có \(n\) đỉnh, \(n>3\). Gọi \(p\) là chu vi của đa giác đó. Chứng minh rằng
\(n-3< \dfrac{2d}{p}< \left[\dfrac{n}{2}\right]\left[\dfrac{n+1}{2}\right]-2\)
(với \(\left[x\right]\) là số nguyên lớn nhất không vượt quá \(x\))
2) Tìm tất cả các hàm số \(f:ℕ^∗\rightarrowℕ^∗\) thỏa mãn điều kiện
\(f\left(x+f\left(y\right)\right)=y+f\left(x+2022\right);\forall x,y\inℕ^∗\)