Cho biết các góc và các cạnh của tứ giác ABCD ở Hình 65 có đặc điểm gì?
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi E , F, G, H lần lượt là các trung điểm của các cạnh AB, BC, CD, DA.
a) Tứ giác EFGH là hình gì.
b) Biết Ac = 10cm, BD = 8cm. Tính diện tích tứ giác EFGH.
c) Cần có điều kiện gì để tứ giác EFGH là hình vuông
Bài 9: Cho tứ giác ABCD. Hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, P, Q lần lượt là
trung điểm của các cạnh AB, BC, CD và DA.
a) Tứ giác MNPQ là hình gì?Vì sao?
b) Để MNPQ là hình vuông thì tứ giác ABCD cần có điều kiện gì?
a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và \(MQ=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình của ΔBCD
Suy ra: NP//BD và \(NP=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC
mà AC\(\perp\)BD
nên MN\(\perp\)BD
hay MN\(\perp\)MQ
Xét tứ giác MQPN có
MQ//NP
MQ=NP
Do đó: MQPN là hình bình hành
mà \(\widehat{QMN}=90^0\)
nên MQPN là hình chữ nhật
B1, Cho tứ giác ABCD có các tia p/giác của góc A và góc D vuông góc với nhau.Chứng minh:
a)ABCD là hình thang
b) Hai tia phân giác của góc C và D vuông góc với nhau
B2, Cho hình thang ABCD có đáy AB=40,CD=80, cạnh bên BC=50,AD=30. Chứng minh ABCD là hình thang vuông
B3.Cho tam giác MNP vuông cân ở M, đường thẳng d bất kỳ qua M ( d không cắt NP). Trên d lấy A,B sao cho MA=PB vàMB=NA. Tứ giác ANPB là hình gì?
B4. Cho ABCD là hình thang có BD là phân giác góc D và AE là p/giác góc A ( E nằm trên CD). Biết AE//BC và Olà giao điểm của AE và DB. Chứng minh:
a) AE vuông góc BD
b) AD//BE và AD=BE
c) E là trung điểm DC
d) Tứ giác BCEO là hình gì?
e) Biết góc BEC=180 độ. Tính các góc ABCD
Mong mọi người giúp với a.! Mình cảm ơn nhiềuuuuuuuuuuuuuu... lắm! :)
Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác của bốn góc vuông có đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì ?
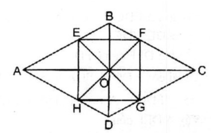
Ta có: ∠ (AOB) và ∠ (COD) đối đỉnh nên E, O, G thẳng hàng
∠ (BOC) và ∠ (AOD) đối đỉnh nên F, O, H thẳng hàng
Xét ∆ BEO và ∆ BFO:
∠ (EBO) = ∠ (FBO) (tính chất hình thoi)
OB cạnh chung
∠ (EOB) = ∠ (FOB) = 45 0 (gt)
Do đó: ∆ BEO = ∆ BFO (g.c.g)
⇒ OE = OF (1)
Xét ∆ BEO và ∆ DGO:
∠ (EBO) = ∠ (GDO) (so le trong)
OB = OD(tính chất hình thoi)
∠ (EOB) = ∠ (GOD) (đối đỉnh)
Do đó: ∆ BEO = ∆ DGO (g.c.g)
⇒ OE = OG (2)
Xét ∆ AEO và ∆ AHO:
∠ (EAO) = ∠ (HAO) (tính chất hình thoi)
OA cạnh chung
∠ (EOA) = ∠ (HOA) = 45 0 (gt)
Do đó: ∆ AEO = ∆ AHO (g.c.g)
⇒ OE = OH (3)
Từ (1), (2) và (3) suy ra: OE = OF = OG = OH hay EG = FH
nên tứ giác EFGH là hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
OE ⊥ OF (tính chất tia phân giác của hai góc kề bù)
hay EG ⊥ FH
Vậy hình chữ nhật EFGH là hình vuông.
1. Cho tam giác ABC có góc A = 90 độ , góc C = 30 độ. Từ trung điểm E của cạnh AB vẽ đường thẳng vuông góc với AB cắt BC ở F.
a) Tứ giác AEFC là hình gì? Vì sao?
b) Tính độ đà các cạnh của tứ giác AEFC, biết AB= 3cm.
2. Cho hình thang ABCD có góc A= góc B = 90 độ ; AB=BC=1/2AD=3cm.
a) Tính các góc của hình thang .
b) Chứng minh AC vuông góc với CD
c) Tính chu vi hình tahng.
3. Chứng minh rằng tứ giác ABCD là hình thang (AD//BC) khi và chỉ khi phân giác của góc Avaf góc B vuông góc với nhau.
4. Cho hình thang cân ABCD có AD//BC, AB = 3cm, CD= 6cm, AD= 2.5cm. Vẽ 2 đường cao AH, BK. Tính DH,DK,AH
Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác của bốn góc vuông có đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì ?
Bài 1: Cho tam giác ABC.Trên AC lấy 1 điểm B' sao cho AB'=AB, trên AC lấy điểm C' sao cho AC'=AC. CMR tứ giác BB'CC' là hình thang.
Bài 2:CMR: nếu 1 tứ giác có phân giác trong của hai góc kề với một cạnh vuông góc với nhau thì tứ giác đó là hình thang.
Bài 3: Cho hình thang ABCD(AB//CD). Hai đường phân giác của góc A và B cắt nhau tại điểm K thuộc cạnh đáy CD:. CM AD+BC=CD.
Bài 4: a)Tính số đo của các góc trong tứ giác ABCD, biết góc A:góc B:góc C:góc D=2:2:1:1.
b)Tứ giác ABCD là hình gì?Vì sao?
Bài 5:Cho tam giác ABC cân tại A. Kẻ các phân giác BD,CE của các góc B và C.
a)Cm: Tam giác ADB= tam giác AEC.
b)Cm: Tứ giác BEDC là hình thang cân có cạnh bên bằng 1/2 đáy.
Bài 6:Cho tam giác ABC vuông tại A có góc ABC=60 độ. Kẻ tia Ax song song với BC.Trên tia Ax lấy điểm D sao cho AD=BC.
a) Tính số đo các góc BAD và BAC.
b)Cm tứ giác ABCD là hình thang cân.
Mình đang cần gấp nên mong các bạn giải giùm mình. ^-^
Bài 1:
a.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = 1800 - D = 1800 - 540 = 1260
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 - C = 1800 - 1050 = 750
b.
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
=> A = (1800 - 320) : 2 = 740
=> D = 1800 - 740 = 1060
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
=> B = 1800 : (1 + 2) . 2 = 1200
=> C = 1800 - 1200 = 600
Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC
Cho tứ giác ABCD.Hai đường chéo AC và BD vuông góc với nhau. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB,BC,CD và DA a) Tứ giác MNPQ là hình gì? vì sao? b) Để MNPQ là hình vuông thì tứ giác ABCD cần có điều kiện gì?
a: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBD có CN/CB=CP/CD
nên NP//BD và NP=BD/2
=>MQ//PN và MQ=PN
=>MNPQ là hình bình hành
Xét ΔBAC có BM/BA=BN/BC
nên MN//AC và MN=AC/2
=>MN vuông góc với NP
=>MNPQ là hình chữ nhật
b: Để MNPQ là hình vuông thì MN=NP
=>AC=BD
Cho tứ giác ABCD .Hai đường chéo AC và BD vuông góc với nhau .Gọi M,N,P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA
a, Tứ giác MNPQ là hình gì? Vì sao ?
b,Để MNPQ là hình vuông thì tứ giác ABCD cần có điều kiện gì ?
Mk ko biết làm bài này khó quá trời
a) tgiác ABC có MN là đường trung bình => MN // AC và MN = AC/2
tgiác DAC có PQ là đường trung bình => PQ // AC và PQ = AC/2
vậy: MN // PQ và MN = PQ => MNPQ là hình bình hành
mặt khác xét tương tự cho hai tgiác ABD và CBD ta cũng có:
NP // BD và NP = BD/2
do giả thiết AC_|_BD => AC_|_NP mà MN // AC => MN_|_NP
tóm lại MNPQ là hình chữ nhật (hbh có một góc vuông)
b) MNPQ là hình vuông <=> MN = NP <=> AC/2 = BD/2 <=> AC = BD
vậy điều kiện là: tứ giác ABCD có hai đường chéo vuông góc và bằng nhau
Tứ giác ABCD có góc A= góc B= góc C= góc D= 90 độ và có AB=BC.
a. Tứ giác ABCD là hình gì? Vì sao?
b.Nếu AC =3cm thì các cạnh của tứ giác ABCD là bao nhiêu cm ?
Mong các bạn ghi rõ ra cho mik mai mik kiểm tra rồi
a/Tứ giác có 4 góc bằng nhau và = 90 độ và 2 cạnh liên tiếp bằng nhau thì tứ giác đó là hình vuông. Vậy ABCD là hình vuông
b/ AC là đường chéo của hình vuông nên
\(AC=AB.\sqrt{2}\Rightarrow AB=\frac{AC}{\sqrt{2}}=\frac{3}{\sqrt{2}}=\frac{3\sqrt{2}}{2}\)