Giải phương trình: 7x2 - 12 x -64
Những câu hỏi liên quan
Giải các phương trình:
x
3
+
7
x
2
+
6
x
-
30
x
3
-...
Đọc tiếp
Giải các phương trình: x 3 + 7 x 2 + 6 x - 30 x 3 - 1 = x 2 - x + 16 x 2 + x + 1
Điều kiện : x ≠ 1
Ta có:
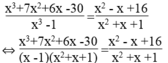
⇔ x 3 +7 x 2 +6x -30 = ( x 2 –x +16)(x -1)
⇔ x 3 +7 x 2 +6x -30 = x 3 – x 2 – x 2 +x +16x -16
⇔ 9 x 2 -11x -14 =0
∆ = - 11 2 -4.9.(-14) = 121 +504 = 625 > 0
∆ ' = 625 =25
Giá trị của x thỏa mãn điều kiện bài toán
Vậy nghiệm của phương trình là x = -7/9 và x = 2
Đúng 0
Bình luận (0)
Giải các phương trình sau:
-
7
x
2
+
4
x
3
+
1
5
x
2
-
x
+
1
-
1...
Đọc tiếp
Giải các phương trình sau: - 7 x 2 + 4 x 3 + 1 = 5 x 2 - x + 1 - 1 x + 1
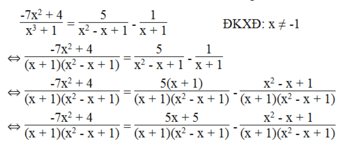
⇔ -7 x 2 + 4 = 5x + 5 – x 2 + x – 1
⇔ -7 x 2 + x 2 – 5x – x = 5 – 1 – 4
⇔ -6 x 2 – 6x = 0
⇔ - x 2 – x = 0
⇔ x(x + 1) = 0
⇔ x = 0 hoặc x + 1 = 0
⇔ x = 0 hoặc x = -1 (loại)
Vậy phương trình có nghiệm x = 0.
Đúng 0
Bình luận (0)
Giải các phương trình sau:
7
x
2
-
14
x
-
5
15
(
2
x
+
1
)
2
5
-
(
x
-
1
)
2...
Đọc tiếp
Giải các phương trình sau: 7 x 2 - 14 x - 5 15 = ( 2 x + 1 ) 2 5 - ( x - 1 ) 2 3
Giải các phương trình sau:a)
x
+
2
x
+
x
−
1
5
3
1
−
3
x
−
1
−
2
x...
Đọc tiếp
Giải các phương trình sau:
a) x + 2 x + x − 1 5 3 = 1 − 3 x − 1 − 2 x 3 5 ;
b) 2 x + 1 2 5 − x − 1 2 3 = 7 x 2 − 14 x − 5 15 .
Giải phương trình:
4x√3x2+1−√x−1=7x2+1
Giải các phương trình 2x4 - 7x2 + 5 = 0
2x4 – 7x2 + 5 = 0 (1)
Tập xác định: D = R.
Đặt t = x2, điều kiện t ≥ 0.
Khi đó phương trình (1) trở thành:
2t2 – 7t + 5 = 0
⇔ (2t – 5) (t – 1) = 0
Đúng 0
Bình luận (0)
Giải phương trình
\(\frac{18^x+32^x-12^x-16^x}{27^x+36^x+48^x+64^x}=\frac{-5}{2x}\)
Viết phương trình về dạng
\(\frac{2^x}{3^x+4^x}-\frac{4^x}{9^x+16^x}=\frac{-5}{2x}\) hay \(\frac{2^x}{3^x+4^x}+\frac{5}{x}=\frac{2^{2x}}{3^{2x}+4^{2x}}+\frac{5}{2x}\)
Xét hàm số \(f\left(t\right)=\frac{2^t}{3^t+4^t}+\frac{5}{t}\) luôn đồng biến
Đáp số : Phương trình vô nghiệm
Đúng 0
Bình luận (0)
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau: 7 x 2 - 2 x + 3 = 0
Phương trình bậc hai: 7x2 – 2x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b2 – 4ac = (-2)2 – 4.7.3 = -80 < 0
Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Giải các phương trình sau: 1)√3x²-√12=0
2)√(x-3)²=9
3)√4x²+4x+1=6
4)√(2x-1)²=3
5)√(x-3)²=3-x 6)√4x²-20x+25+2x=5
7)√1-12x+36x²=5
1.
$\sqrt{3x^2}-\sqrt{12}=0$
$\Leftrightarrow \sqrt{3x^2}=\sqrt{12}$
$\Leftrightarrow 3x^2=12$
$\Leftrightarrow x^2=4$
$\Leftrightarrow (x-2)(x+2)=0\Leftrightarrow x=\pm 2$
Đúng 0
Bình luận (0)
2.
$\sqrt{(x-3)^2}=9$
$\Leftrightarrow |x-3|=9$
$\Leftrightarrow x-3=9$ hoặc $x-3=-9$
$\Leftrightarrow x=12$ hoặc $x=-6$
Đúng 0
Bình luận (0)
3.
$\sqrt{4x^2+4x+1}=6$
$\Leftrightarrow \sqrt{(2x+1)^2}=6$
$\Leftrightarrow |2x+1|=6$
$\Leftrightarrow 2x+1=6$ hoặc $2x+1=-6$
$\Leftrightarrow x=\frac{5}{2}$ hoặc $x=\frac{-7}{2}$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời