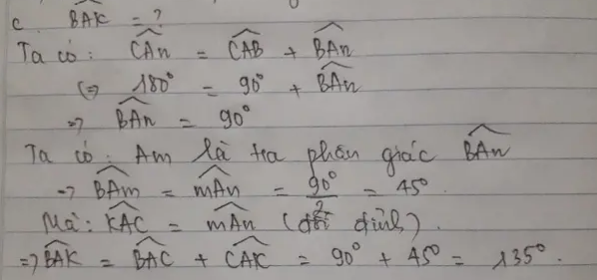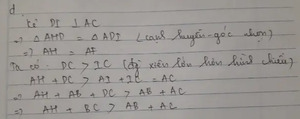Trên đường phân giác của góc ngoài đỉnh C của ΔABC, lấy một điểm D ≠ C. CMR: AD+BD > AC+BC

Những câu hỏi liên quan
cho ΔABC vuông tai A, vẽ đường cao AH, trên cạnh BC lấy điểm D sao cho BD=BA, đường vuông góc vs BC tại D cắt AC ở E
a) CM: AE=DE
b) CM: AD là tia phân giác của góc HAC
c) so sánh HD và DC
d) đường p/giác góc ngoài tại đỉnh C cắt đường thẳng BE ở K. tính BAK
a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
Do đó:ΔBAE=ΔBDE
Suy ra: EA=ED
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là phân giác của góc HAC
Đúng 1
Bình luận (0)
Cho tam giác ABC có góc A=90 độ, đường cao AH. Trên cạnh BC lấy D sao cho BD=BA. Đường thẳng vuông góc với BC tại D cắt AC tại E
a) CMR: AE=ED.
b) CMR: tia AD là tia phân giác của góc HAC.
c) Đường phân giác của góc ngoài tại đỉnh C cắt đường thẳng BE tại K. Tính góc BAK.
d) CMR: AB+AC<BC+AH
e) So sánh HD và DC
a) ΔABDΔABD cân tại A => BADˆ=BDAˆBAD^=BDA^ (t/c tam giác cân)
Lại có: BADˆ+DAEˆ=BACˆ=90oBAD^+DAE^=BAC^=90o
BDAˆ+ADEˆ=BDEˆ=90oBDA^+ADE^=BDE^=90o
Do đó, DAEˆ=ADEˆDAE^=ADE^
=> ΔADEΔADE cân tại E (dấu hiệu nhận biết tam giác cân)
=> AE = ED (t/c tam giác cân) (đpcm)
b) Có: AH // ED (cùng ⊥BC⊥BC)
=> HADˆ=ADEˆHAD^=ADE^ (so le trong)
= DAE (câu a)
=> AD là phân giác HACˆ(đpcm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC , góc A = 90o . Đường cao AH. Trên cạnh BC lấy điểm D sao cho BD = BA . Đường vuông góc với BC tại D cắt AC ở E .
a) So sánh : AD là tia phân giác của góc HAC
b) Đường phân giác góc ngoài đỉnh C cắt đường thẳng BE tại K . Tính góc BAK ?
c) So sánh : HD và DC
d) CMR : AB + AC < BC + AH
1. Cho tam giác ABC có góc A=90 độ. Đường cao AH. Trên cạnh BC lấy D sao cho BD=BA. Đường vuông góc với BC tại D cắt AC tại E a) So sánh AE và DE
b) CMR : Tia AD là tia phân giác của góc HAC
c) Đường phân giác góc ngoài đỉnh C cắt đường thẳng BC ở K. Tính BAK
d) CMR : AB + AC < BC + AH
e) So sánh HD và DC
a) ΔABDΔABD cân tại A => BADˆ=BDAˆBAD^=BDA^ (t/c tam giác cân)
Lại có: BADˆ+DAEˆ=BACˆ=90oBAD^+DAE^=BAC^=90o
BDAˆ+ADEˆ=BDEˆ=90oBDA^+ADE^=BDE^=90o
Do đó, DAEˆ=ADEˆDAE^=ADE^
=> ΔADEΔADE cân tại E (dấu hiệu nhận biết tam giác cân)
=> AE = ED (t/c tam giác cân) (đpcm)
a) Có: AH // ED (cùng ⊥BC⊥BC)
=> HADˆ=ADEˆHAD^=ADE^ (so le trong)
= DAE (câu a)
=> AD là phân giác HACˆ(đpcm)
Cho ΔABC , góc A =90 độ , góc B=60độ .
a, So sánh AD và BD
b, Trên BC lấy D sao cho BD=AB . Qua D dựng đường vuông góc với BC cắt tia đối của AB tại E . Chứng minh : ΔABC=ΔDBE
c, H là giao điểm của AC và ED . Chứng minh : BH là phân giác của góc ABC
d, Qua B vẽ đường thẳng vuông góc AB cắt ED tại K . Chứng minh : ΔHBK đều
b) Xét ΔABC vuông tại A và ΔDBE vuông tại D có
AB=BD(gt)
\(\widehat{ABC}\) chung
Do đó: ΔABC=ΔDBE(cạnh góc vuông-góc nhọn kề)
c) Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
BA=BD(gt)
Do đó: ΔBAH=ΔBDH(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ABH}=\widehat{DBH}\)(hai góc tương ứng)
hay BH là tia phân giác của \(\widehat{ABC}\)
d) Ta có: BH là tia phân giác của \(\widehat{ABC}\)(cmt)
nên \(\widehat{ABH}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: \(\widehat{ABH}+\widehat{HBK}=90^0\)
\(\Leftrightarrow\widehat{HBK}+30^0=90^0\)
hay \(\widehat{HBK}=60^0\)
Xét ΔCHD vuông tại D và ΔCBA vuông tại A có
\(\widehat{ACB}\) chung
Do đó: ΔCHD\(\sim\)ΔCBA(g-g)
Suy ra: \(\widehat{CHD}=\widehat{CBA}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{CHD}=60^0\)
mà \(\widehat{CHD}=\widehat{HKB}\)(hai góc so le trong, BK//AC)
nên \(\widehat{HKB}=60^0\)
Xét ΔHBK có
\(\widehat{HKB}=60^0\)(cmt)
\(\widehat{HBK}=60^0\)(cmt)
Do đó: ΔHBK đều(Dấu hiệu nhận biết tam giác đều)
Đúng 0
Bình luận (1)
Cho ΔABC có góc A=90o . Kẻ AH vuông góc với BC tại H . Trên cạnh BC lấy D sao cho BD = BA . Đường vuông góc với BC tại D cắt AC ở E.
a) So sánh AE và DE
b) Chứng minh tia AD là tia phân giác của góc HAC
c) Đường phân giác của góc ngoài đỉnh C cắt đường thẳng BE ở K . Tính góc BAK
=> Mọi người giúp mk nha
a) Có góc DBH = góc AHB ( cùng = 90 º do cùng vuông góc BC ) mà 2 góc này ở vị trí so le trong nên BD song song AH.
Lại có BD = AH ( gt ) nên AHBD là hbh , vậy AB song song DH ( theo tính chất hbh )
b) Xét tam giác ABH có góc BAH = 35 º ( gt ) , góc AHB = 90 º do AH vuông góc BC.
Vậy góc ABC = 180º-90º-35º = 55º .
Do đó góc ACB = 180º - góc ABC - góc BAC
= 180º-90º-55º = 35º
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A ( AB<AC). Trên cạnh BC lấy điểm D sao cho BD=BA. Đường vuông góc với BC cắt AC ở E
a)Đường phân giác góc ngoài đỉnh C cắt đường thẳng BE ở K. Tính số đo góc BAK
b) CM: AD=DE
Cho tam giác ABC vuông tại A, đường cao AH. Trên cạnh BC lấy điểm D sao cho BD=BA. Đường vuông góc với BC tại D cắt AC ở E
a) Chứng minh : AE=DE
b)C/m : AD là tia phân giác của góc HAC
c) So sánh : HD và DC
d) Đường phân giác góc ngoài tại đỉnh C đường thẳng BE ở K . Tính góc BAK ?
Cho tam giác ABC vuông tại A. Đường cao AH trên cạnh BC lấy điểm D sao cho BD=BA, đường vuông góc voi BC tại D cắt AC tại E.
a, So sánh AD và DE
b, chứng minh :AD là phân giác góc HAC
c, đường phân giác ngoài đỉnh C cắt đường thẳng BE ở K.Tính góc BAK
d, chứng minh : AB+AC<BC+AH; DH<DC